Week 7: Heap & Priority Queue (ADT)

Heaps
Heap Applications
Download the source files

Heaps

Heap is a very useful data structure with many applications (e.g Heapsort and Priority Queues (ADT)). Heap elements are typically allocated as a dynamic array. However, the elements are conceptually forming a complete tree.

Max-Heap Logical Representation

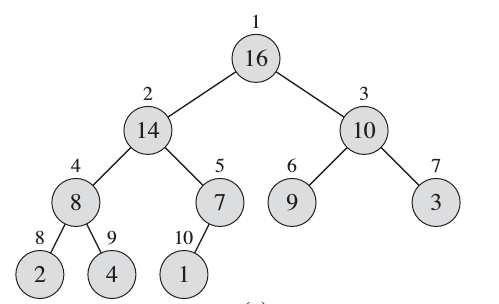Max-Heap Storage

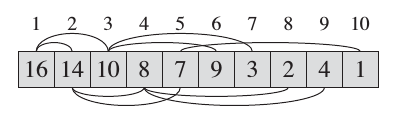Max-Heap

Creative Commons - Maxinator

Heap Applications

Sorting Algorithms (Heapsort)
The Shortest Path Problem (Dijkstra’s Algorithm)
Data Compression Algorithms (Huffman Tree)
Unsupervised Machine Learning (Agglomerative Clustering)

Glossary

Complete Tree: A balanced tree in which the distance from the root to any leaf is either $\lfloor \log(n) \rfloor$ or $\lfloor \log(n)-1 \rfloor$. source.

Operations

Insert

Inserting an element at the end of the heap typically violates the heap property (i.e each parent is greater than its children for max-heaps), so after each insertion we need to recover back the heap property.

The algorithm of insertion (source: wikipedia):

Insert the new element to the bottom level of the heap.
Compare the added element with its parent; if they are in the correct order, stop.
If not, swap the element with its parent and repeat step (2) recursively.

Example: Insert 15

Steps	Layout
We first place the new element 15 in the position marked by the X as a leaf.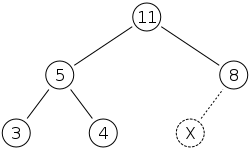
However, the heap property is violated since 15 > 8, so we need to swap the 15 and the 8
The heap property is still violated since 15 > 11, so we need to swap again
Source: wikipedia

Extract

In a similar way to insertion, when we pop the maximum of max-heap (its root), we violate the heap property by replacing the last children in the heap to be the new root. In order to recover the heap property, we use the following procedures (source: wikipedia):

Replace the root of the heap with the last element on the last level.
Compare the new root with its children; if they are in the correct order, stop.
If not, swap the element with one of its children and repeat step (2). (Swap with its smaller child in a min-heap and its larger child in a max-heap.)

Steps	Layout
Extract element 11.
11 is replaced by the the left-most leaf 4.
Heap property is violated (8 is greater than 4). Swapping the two elements 4 and 8 is enough to recover the heap.
Source: wikipedia

Min-heap Implementation Using Arrays

Implementation: Class Members

template< typename T >
class Heap
{
public:
    size_t size() const
    {
        // Return heap size
    }

    void insert(T value)
    {
        // 1. Insert as leaf
        // 2. Recover heap properties
    }

    T extract()
    {
        // 1. Extract the root
        // 2. Recover heap properties
    }
private:
    // Private methods
private: 
    // Private data members
};

Implementation: Storage Array

template< typename T >
class Heap
{
public:
    // Return heap size
    size_t size() const {}

    // 1. Insert as leaf
    // 2. Recover heap properties
    void insert(T value){}

    // 1. Extract the root
    // 2. Recover heap properties
    T extract(){}
private:
    // Private methods
private: 
    // Private data members
    std::vector< T > data;
};

Implementation: From Parent Index to Child Index + Vice versa

template< typename T >
class Heap
{
public:
    // Return heap size
    size_t size() const {}

    // 1. Insert as leaf
    // 2. Recover heap properties
    void insert(T value){}

    // 1. Extract the root
    // 2. Recover heap properties
    T extract(){}
private:
    // Private methods
    static size_t leftChildIdx(size_t parent)
    {
        return parent * 2 + 1;
    }

    static size_t rightChildIdx(size_t parent)
    {
        return parent * 2 + 2;
    }

    static size_t parentIdx(size_t child)
    {
        if (child % 2 == 1)
            return (child - 1) / 2;
        else
            return (child - 2) / 2;
    }
private: 
    // Private data members
    std::vector< T > data;
};

Implementation: Heap size

template< typename T >
class Heap
{
public:
    // Return heap size
    size_t size() const { return data.size();}

    // 1. Insert as leaf
    // 2. Recover heap properties
    void insert(T value){}

    // 1. Extract the root
    // 2. Recover heap properties
    T extract(){}
private:
    // Private methods
    static size_t leftChildIdx(size_t parent){... }
    static size_t rightChildIdx(size_t parent){... }
    static size_t parentIdx(size_t child){... }
private: 
    // Private data members
    std::vector< T > data;
};

Implementation: Insert & SiftUp

The insert operation adds a new node as the left-most leaf
To recover the heap properties the siftUp is applied on the new node: if node is greater than its parent, then heap is satisfied and terminate, otherwise, swap the node with parent and repeat recursively.

Worst case time: to go up along all levels $h= \lfloor \log(n) \rfloor$.
$O(T(n)) = O(h) = O(\log(n))$

template< typename T >
class Heap
{
public:
    // Return heap size
    size_t size() const { return data.size();}

    void insert(T value)
    {
        data.push_back(value);
        size_t childIdx = size() - 1;
        siftUp( childIdx ); // Recover heap
    }

    // 1. Extract the root
    // 2. Recover heap properties
    T extract(){}
private:
    // Private methods
    void siftUp( size_t child )
    {
        auto parent = parentIdx(child);
        if( child > 0  && data[child] < data[parent])
        {
            std::swap(data[child], data[parent]);
            siftUp( parent );
        }
    }

    static size_t leftChildIdx(size_t parent){... }
    static size_t rightChildIdx(size_t parent){... }
    static size_t parentIdx(size_t child){... }
private: 
    // Private data members
    std::vector< T > data;
};

Implementation: Extract & SiftDown

The extract operation removes the root and replace it by the left-most leaf.
To recover the heap properties the siftDown is applied on the new root: if root is less than its children, then heap is satisfied and terminate, otherwise, swap the root with the minimum children and repeat recursively.

Worst case time: to go down along all levels $h= \lfloor \log(n) \rfloor$.
$O(T(n)) = O(h) = O(\log(n))$

template< typename T >
class Heap
{
public:
    // Return heap size
    size_t size() const { return data.size();}

    void insert(T value){... }

    // 1. Extract the root
    // 2. Recover heap properties
    T extract()
    {
        if( data.empty())
        {
            std::cout << "Empty Heap!\n";
            exit( 1 ); // Crash
        }
        size_t child = size() - 1;
        std::swap(data[child], data[0]);
        T value = data.back();
        data.pop_back();
        siftDown(0);
        return value;
    }
private:
    // Private methods
    void siftUp( size_t child ){... }

    void siftDown( size_t parent)
    {
        size_t left = leftChildIdx(parent);
        size_t right = rightChildIdx(parent);
        size_t length = size();
        size_t minimum = parent;

        if (left < length && data[left] < data[minimum])
            minimum = left;

        if (right < length && data[right] < data[minimum])
            minimum = right;

        if (minimum != parent)
        {
            std::swap(data[minimum], data[parent]);
            siftDown( minimum );
        }
    }

    static size_t leftChildIdx(size_t parent){... }
    static size_t rightChildIdx(size_t parent){... }
    static size_t parentIdx(size_t child){... }
private: 
    // Private data members
    std::vector< T > data;
};

Implementation: Heapifying Arbitrary Array

template< typename T >
class Heap
{
public:
    size_t size() const{... }
    void insert(T value){... }
    T extract(){... }

    static Heap make( std::vector< T > data )
    {
        Heap h;
        h.data.swap( data ); // O(1)
        if( h.size() <= 1 ) return h;

        auto lastChild = h.size() - 1;
        for( int subHp = parentIdx( lastChild ); subHp >= 0 ; --subHp )
            h.siftDown( subHp );
        return h;
    }
private:
    // Private methods
    void siftUp( size_t child ){... }
    void siftDown( size_t parent){... }
    static size_t leftChildIdx(size_t parent){... }
    static size_t rightChildIdx(size_t parent){... }
    static size_t parentIdx(size_t child){... }
private: 
    // Private data members
    std::vector< T > data;
};

Complexity Analysis: Heapifying Arbitrary Array

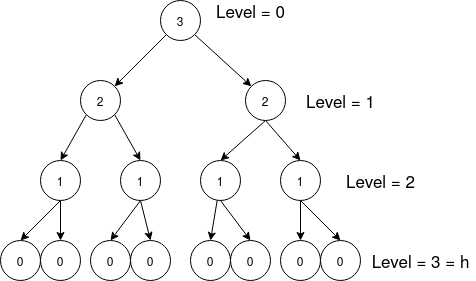
Level	#Sub_Heaps	Heapify Cost
$h$	$2^h$	0
$h-1$	$2^{h-1}$	1
…	…	…
1	2	$h-1$
0	1	$h$

Time Growth Function $T(n)$ for heapifying all nodes:

\[T(n) = 2^h \times 0 + 2^{h-1} \times 1 + \ldots + 2^0 \times h = \sum_{j=0}^h j 2^{h-j} \label{eq:tn}\tag{E1}\]

Useful Equations

The relation between
- $h$: the height of a full binary tree and
- $n$: the number of nodes:

\[\begin{align*} n &= 1 + 2 + 4 + \ldots + 2^h \\ n + 1 &= (1 + 1) + 2 + 4 + \ldots + 2^h \\ n + 1 &= (2 + 2) + 4 + \ldots + 2^h \\ &\vdots \\ n + 1 &= 2^h + 2^h = 2^{h+1} \label{eq:nh}\tag{E2} \end{align*}\]

The power series: $\begin{equation} \sum_{j=0}^{\infty} x^j = \frac{1}{1-x}; |x|<1 \label{eq:PS1}\tag{PS1} \end{equation}$
Differentiating Equation \eqref{eq:PS1} with respect to $x$ yields: $\begin{align*} \sum_{j=0}^{\infty} j x^{j-1} &= \frac{1}{(1-x)^2} \\ \quad &\textrm{multiplying by x:} \quad \\ \sum_{j=0}^{\infty} j x^{j} &= \frac{x}{(1-x)^2} \label{eq:PS2}\tag{PS2} \end{align*}$

Evaluating $T(n)$ & $O(n)$

From \eqref{eq:tn} we estimated $T(n)$ as: $\begin{align*} T(n) &= \sum_{j=0}^h j 2^{h-j} \\ &= \sum_{j=0}^h j \frac{2^h}{2^j} \\ &= 2^h \sum_{j=0}^h \frac{j}{2^j} \\ \textrm{by substituting $x=\frac{1}{2}$ in \eqref{eq:PS2}:} \\ \sum_{j=0}^\infty \frac{j}{2^j} &= \sum_{j=0}^\infty j(\frac{1}{2})^j = \frac{\frac{1}{2}}{(1 - \frac{1}{2})^2} = 2 \\ \textrm{therefore: }& \\ 2^h \sum_{j=0}^h \frac{j}{2^j} &< 2^h \sum_{j=0}^\infty \frac{j}{2^j} = 2^h (2) \\ \textrm{therefore: } & \\ T(n) &< 2^{h+1} \\ \textrm{From \eqref{eq:nh}: } & \\ T(n) &< n + 1 \\ \textrm{therefore, the big-O notation of $T(n)$:}& \\ O(T(n)) &= O(n) \end{align*}$

Reference (Heapify Analysis and O(n) derivation): Lecture 14: HeapSort Analysis and Partitioning - CMSC 251

Final Implementation of Heap

Heap Applications: Heapsort

std::vector< int > heapSort( std::vector< int > a )
{
    auto h = Heap<int>::make( a ); // Heapify: O(n)
    a.clear();
    while( h.size() > 0 ) // O( n * log(n) )
        a.push_back( h.extract()); // O(log(n))
    return a;
}

Time Complexity: $O(T(n)) = O(n) + O(n\log(n)) = O(n\log(n))$

Advanced: avoiding $O(n)$ deep copy

std::vector< int > heapSort( std::vector< int > a )
{
    auto h = Heap<int>::make( std::move( a ));
    while( h.size() > 0 )
        a.push_back( h.extract());
    return a;
}

The first line in this function avoids making a deep copy of std::vector<int>. Also, a becomes empty after that line (very briefly: some other std::vector<int> has stolen the pointer to the internal raw array of a, and then updated a internal pointer to nullptr)

To understand what is happening:

Visualization & Links

Heapsort

Heaps and Heap Sort

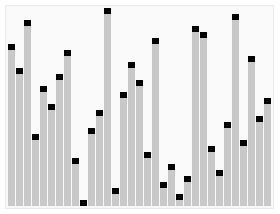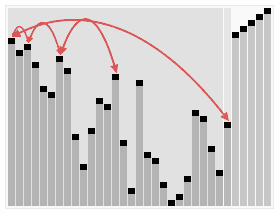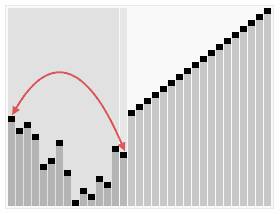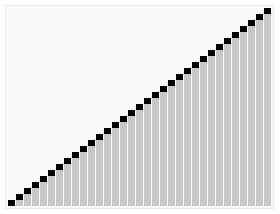Download the source files

mkdir -p section07/Heap
cd section07/Heap
wget -i https://raw.githubusercontent.com/sbme-tutorials/sbme-tutorials.github.io/master/2020/data-structures/snippets/section07/Heap/download.txt

To build:

mkdir build
cd build
cmake ..
make