Week 5-a: Recursion
Recursion
One way to describe repetition within a computer program is the use of loops, An entirely different way to achieve repetition is through a process known as recursion.
Recursion is a technique by which a method makes one or more calls to itself during execution, or by which a data structure relies upon smaller instances of the very same type of structure in its representation. There are many examples of recursion in art and nature. For example, fractal patterns are naturally recursive.
The factorial function
To demonstrate the mechanics of recursion, we begin with a simple mathematical example of computing the value of the factorial function. The factorial of a posi- tive integer n, denoted n!, is defined as the product of the integers from 1 to n.
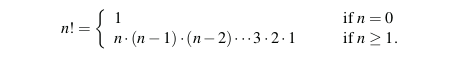
There is a natural recursive definition for the factorial function. To see this, observe that 5! = 5 · (4 · 3 · 2 · 1) = 5 · 4!. More generally, for a positive integer n, we can define n! to be n · (n − 1)!. This recursive definition can be formalized as.

public class factorial {
public static int iterativeFactorial(int n) throws IllegalArgumentException {
if (n < 0) {
throw new IllegalArgumentException();
} else if (n == 0) {
return 1;
} else {
int fact = 1;
for (int i = 1; i <= n; i++)
fact *= i;
return fact;
}
}
public static int recursiveFactorial(int n) throws IllegalArgumentException {
if (n < 0) {
throw new IllegalArgumentException();
} else if (n == 0) {
return 1;
} else {
return n * recursiveFactorial(n - 1);
}
}
public static void main(String[] args) {
System.out.println("#### 5! using loops ####");
System.out.println(factorial.iterativeFactorial(5));
System.out.println("#### 5! using recursion ####");
System.out.println(factorial.recursiveFactorial(5));
}
}
Binary Search
we describe a classic recursive algorithm, binary search, used to efficiently locate a target value within a sorted sequence of n elements stored in an array. This is among the most important of computer algorithms, and it is the reason that we so often store data in sorted order

When the sequence is unsorted, the standard approach to search for a target value is to use a loop to examine every element, until either finding the target or exhausting the data set. This algorithm is known as linear search, or sequential search, and it runs in O(n) time (i.e., linear time) since every element is inspected in the worst case.
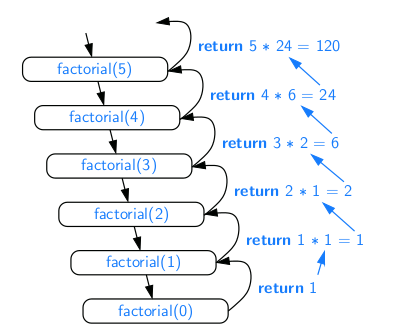
When the sequence is sorted and indexable, there is a more efficient algorithm. (For intuition, think about how you would accomplish this task by hand!) If we consider an arbitrary element of the sequence with value v, we can be sure that all elements prior to that in the sequence have values less than or equal to v, and that all elements after that element in the sequence have values greater than or equal to v. This observation allows us to quickly “home in” on a search target using a variant of the children’s game “high-low.” We call an element of the sequence a candidate if, at the current stage of the search, we cannot rule out that this item matches the target. The algorithm maintains two parameters, low and high, such that all the candidate elements have index at least low and at most high. Initially, low = 0 and high = n − 1. We then compare the target value to the median candidate, that is, the element with index
mid = ⌊(low + high)/2⌋
Complexity O(log n)
We have four cases:
- If the target equals the median candidate, then we have found the item we are looking for, and the search terminates successfully.
- If the target is less than the median candidate, then we recur on the first half of the sequence, that is, on the interval of indices from low to mid − 1.
- If the target is greater than the median candidate, then we recur on the second half of the sequence, that is, on the interval of indices from mid + 1 to high.
- If low > high, as the interval [low, high] is empty. the search failed.
public class BinarySearch {
public static boolean binarySearch(int[] data, int target, int low, int high) {
if (low > high)
return false;
else {
int mid = (low + high) / 2;
if (target == data[mid])
return true;
else if (target < data[mid])
return binarySearch(data, target, low, mid - 1); // recur left of the middle
else
return binarySearch(data, target, mid + 1, high); // recur right of the middle
}
}
}
Linear Recursion:
If a recursive method is designed so that each invocation of the body makes at most one new recursive call, this is know as linear recursion. Of the recursions we have seen so far, the implementation of the Factorial method and Binary Search.
Summing the Elements of an Array Recursively
Linear recursion can be a useful tool for processing a sequence, such as a Java array. Suppose, for example, that we want to compute the sum of an array of n integers. We can solve this summation problem using linear recursion by observing that if n = 0 the sum is trivially 0, and otherwise it is the sum of the first n − 1 integers in the array plus the last value in the array.

public static int linearSum(int[] data, int n) {
if (n == 0)
return 0;
else
return linearSum(data, n - 1) + data[n - 1];
}
Reversing a Sequence with Recursion
Let us consider the problem of reversing the n elements of an array, so that the first element becomes the last, the second element becomes second to the last, and so on. We can solve this problem using linear recursion, by observing that the reversal of a sequence can be achieved by swapping the first and last elements and then recursively reversing the remaining elements.
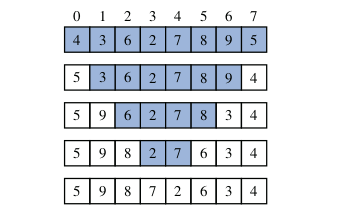
public static void reverseArray(int[] data, int low, int high) {
if (low < high) {
// if at least two elements in subarray
int temp = data[low];
// swap data[low] and data[high]
data[low] = data[high];
data[high] = temp;
reverseArray(data, low + 1, high - 1);
// recur on the rest
}
}
Binary Recursion:
When a method makes two recursive calls, we say that it uses binary recursion
Summing the Elements of an Array Recursively
let us revisit the problem of summing the n integers of an array. Computing the sum of one or zero values is trivial. With two or more values, we can recursively compute the sum of the first half, and the sum of the second half, and add those sums together.

public static int binarySum(int[] data, int low, int high) {
if (low > high)
return 0;
else if (low == high)
return data[low];
else {
int mid = (low + high) / 2;
return binarySum(data, low, mid) + binarySum(data, mid + 1, high);
}
}
HINT:The size of the range is divided in half at each recursive call, and so the depth of the recursion is 1 + logn. Therefore, binarySum uses O(logn) amount of additional space, which is a big improvement over the O(n) space used by the linearSum