Projection
- Projection
- Defining Camera Coordinates
- Pipeline
- Projection Demo
- Animation Using timer function
- Download Demo
Projection
3D projection is mapping a 3 dimensional points to a 2D plane.
Types of projection
- Parallel Projection (Orthogonal)
It preserves the parallelism where parallel lines still parallel by just dropping the Z dimension
\[\begin{bmatrix} x' \\ y' \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\]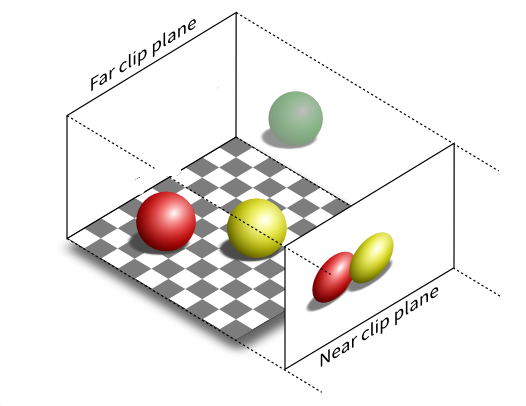
- Perspective Projection
It does not preserve parallelism due to that parallel lines will converge to a single point (Vanishing point).
In perspective projection nearer objects are larger and further are smaller.
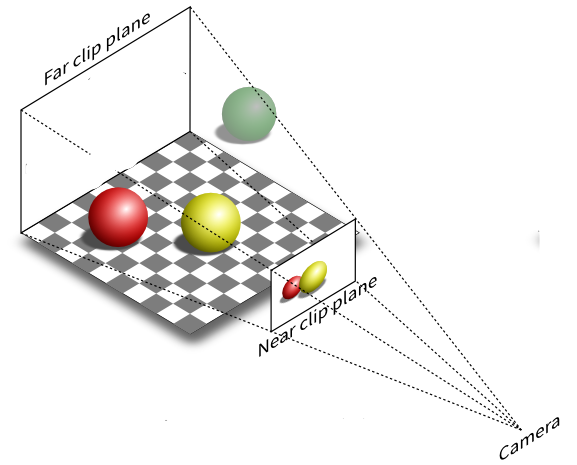
Think of at as a scaling transformation.
\[\begin{bmatrix} \frac{f}{aspect} & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & \frac{Z_{far} + Z_{near}}{Z_{far} - Z_{near}} & \frac{2 * Z_{far} * Z_{near}}{Z_{far} - Z_{near}} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}\]Where
\[f = cot(\frac{fov_y}{2})\]Defining Projection Plane
To identify the projection plane you have to define its width, hight, near and far projections.
To Do that in OpenGL you have two ways
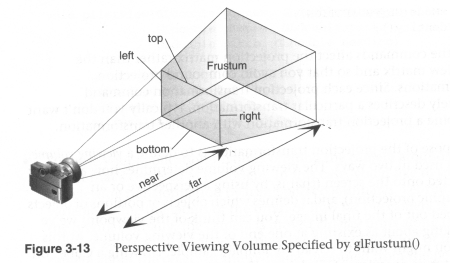
- Using glFrustum
void glFrustum( GLdouble left,
GLdouble right,
GLdouble bottom,
GLdouble top,
GLdouble nearVal,
GLdouble farVal);
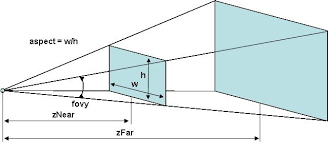
- Using glPerspective
void gluPerspective( GLdouble fovy,
GLdouble aspect,
GLdouble zNear,
GLdouble zFar);
Defining Camera Coordinates
We can define the camer coordintes in OpenGL using
void gluLookAt( GLdouble eyeX,
GLdouble eyeY,
GLdouble eyeZ,
GLdouble centerX,
GLdouble centerY,
GLdouble centerZ,
GLdouble upX,
GLdouble upY,
GLdouble upZ);

Note:
For up direction we care about the sign (Direction of the vector).
Pipeline
Assembly line from set of vertices to set of pixels (image).

The pipeline simply includes
-
3D Modeling (Primitives or vertices) Model (World Coordinates)
-
Lightening and coloring calculations
-
Transform to 3D camera coordinates View (Camera Coordinates)
-
Clip to 2D Screen coordinates Projection (Sceen Coordinate)

Projection Demo
- Projection and camera positioning
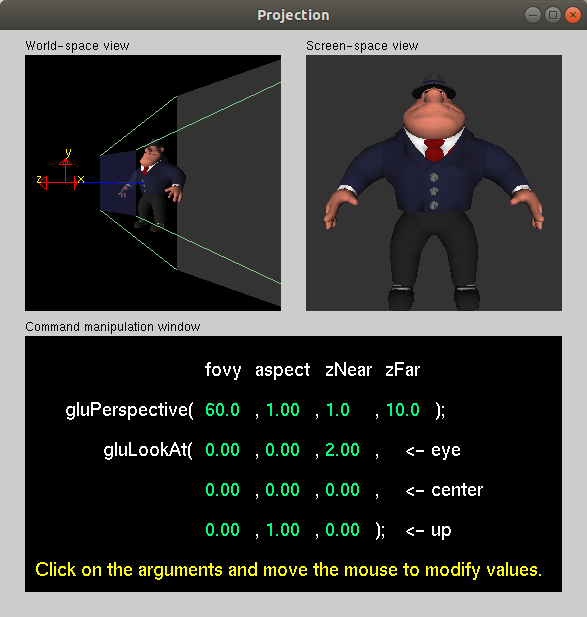
- Pipeline
Each Object is a set of points
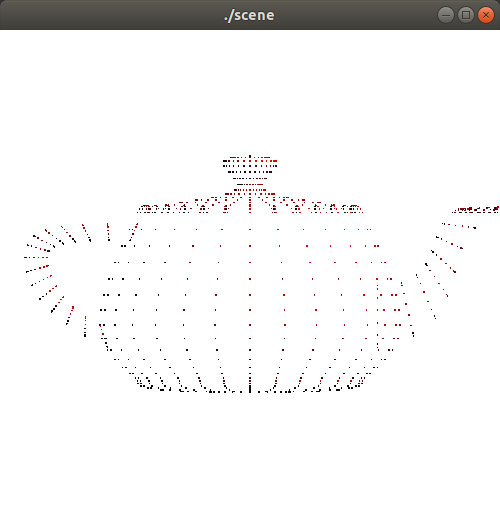
This points are connected together to make a polygon or a mesh

These meshes are colored and lightened.

Animation Using timer function
- Solar system demo.
Rotation of planet around the sun and around itself at the same time using timer function.

Download Demo
All demos will be available in this repository