Transformations

Changing object

  • Position
  • Size
  • Orientation
  • Shape

Transformation is basically a matrix multiplication process and it represents the core of computer graphics.

Translation

Changing position of the object

\(x' = x + t_x\) \(y' = y + t_y\)

\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}\]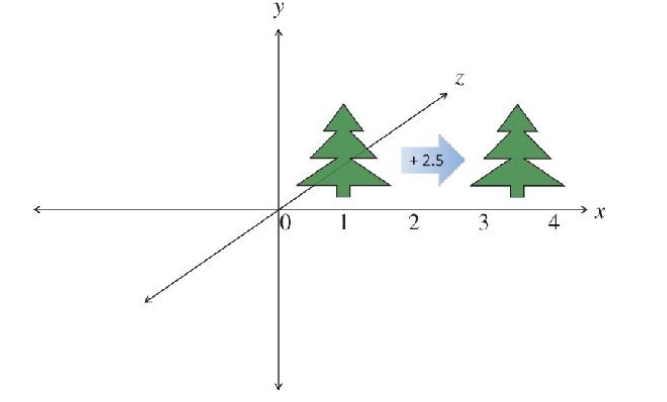

Homogeneous Coordinates

  • Adding additional dimension (Projection dimension) to current coordinate system

  • 2D Cartesian coordinate (x, y) maps to (x, y, w) homogeneous coordinate

  • 3D Cartesian coordinate (x, y, z) maps to (x, y, z, w) homogeneous coordinate For w = 1 homogeneous coordinates is equivalent to cartesian coordinates

Advantages of homogeneous coordinates

  • Make a standard (4x4) matrix shape for all vector operations including
    • Translation
    • Rotation
    • Scaling
    • Perspective Projection (Projection lecture)
  • Sequence of operation will be represented as a single matrix that will be multiplied by the vector or points.

Translation in Homogeneous coordinates

Let w = 1 for now Transformation matrix is 4x4 matrix

\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\]

Scaling

Multiplying by a scale factor

\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\]

Fixed point scaling

  • Scaling operation includes translation
  • It will affect the position of the object and this is undesired effect
  • Scaling must be independent of translation. Solution
    1. Select a point to be fixed
    2. Translate it to origin (So multiplying by zero is zero)
    3. Apply scaling
    4. Translate back to that point
\[P' = (T^{-1} ST)P\]

Rotation

For anticlockwise rotation in 2D coordinates

\[x' = xcos(\theta) - y sin(\theta)\] \[y' = xsin(\theta) + y cos(\theta)\]

For 3D rotation we need to specify rotation access

\[R_z(\theta) = \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 & 0 \\ sin(\theta) & cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\]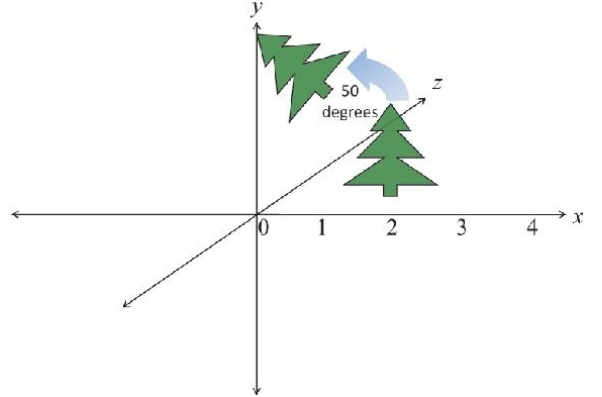

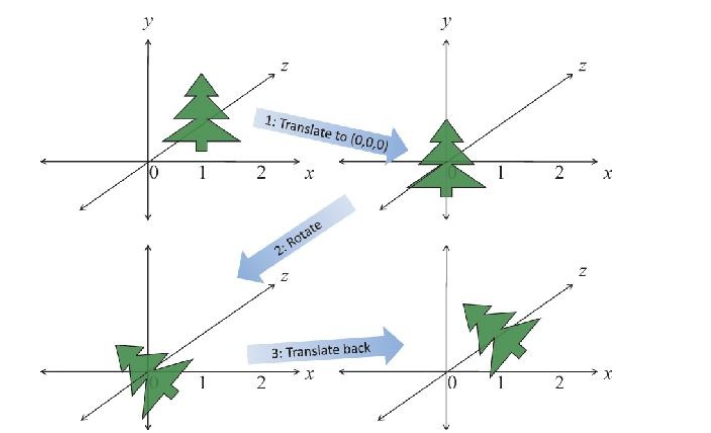
Fixed Point Rotation

  • Same concept as fixed point scaling
  • Select a point to be fixed during rotation Apply the following transformation matrices
\[P' = T^{-1} RT P\]
  • Where T is the translation of selected fixed point to origin.

Notes :

  • Rotation matrix is orthogonal
\[RR^T = I\] \[R^T = R^{-1}\]
  • Reflection is 180 degree rotation.

Transformation in OpenGL

  • OpenGL is a state Machine
  • There is a Current matrix (CM) that holds the current state
  • There is a stack to save different states to use it when needed.
  • glTranslate — multiply the current matrix by a translation matrix (CM = CM*T)
  • glScale — multiply the current matrix by a Scaling matrix (CM = CM*S)
  • glRotate — multiply the current matrix by a Rotation matrix (CM = CM*R)

Note :

Post multiplication is applied (Right side not left side)

Model, View, Projection

  • In World coordinates (Object) we draw our model
  • In view coordinate we put it in camera coordinates
  • In projection coordinates 3D object is projected on screen coordinate
  • We handle this in openGL by setting this matrix mode sequence
glMatrixMode(GL_PROJECTION);
glMatrixMode(GL_MODELVIEW);

More about this in next lectures

Current state Manipulation

  • To save the current state 
    glPushMatrix()
  • To restore that state 
    glPopMatrix()

    To reset your current matrix

    glLoadIdentity()

Cube Example

Translation and rotation Which first ?

Robotic Arm

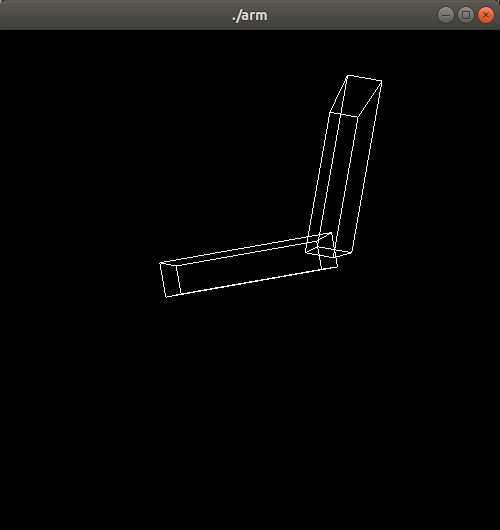
First Exercise

  • Complete the robotic arm
  • Draw its fingers

Section Demo

All demos will be available in this repository