Week 7: Midterm Revision
Midterm Sample Questions
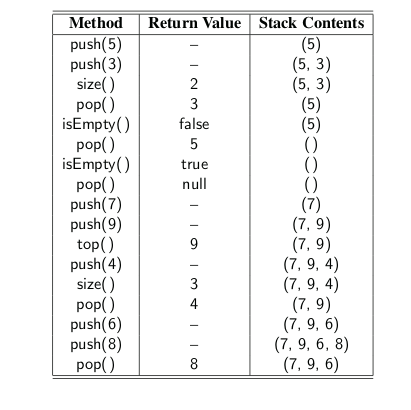
- Q1 What values are returned during the following series of stack operations, if exe- cuted upon an initially empty stack?
Solution
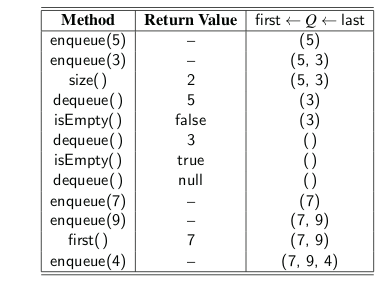
- Q2 What values are returned during the following sequence of queue operations, if executed on an initially empty queue?
Solution
- Q3 Suppose an initially empty queue Q has performed a total of 32 enqueue operations, 10 first operations, and 15 dequeue operations, 5 of which returned null to indicate an empty queue. What is the current size of Q?
Solution
The current size of the Queue is 22.
- Q4 Suppose an initially empty stack S has performed a total of 25 push operations, 12 top operations, and 10 pop operations, 3 of which returned null to indicate an empty stack. What is the current size of S?
Solution
The current size of the Stack is 18.
- Q5 Suppose Alice has picked three distinct integers and placed them into a stack S in random order. Write a short, straightline piece of pseudocode (with no loops or recursion) that uses only one comparison and only one variable x, yet that results in variable x storing the largest of Alice’s three integers with probability 2/3. Argue why your method is correct.
Solution
x = S.pop()
if (x < S.top()){
x = S.pop()
if (x < S.top())
x = S.pop()
}else{
S.pop()
if (x < S.top())
x = S.pop()
}
x is the largest interger
let x equal to stack first elment
if x is less than top of stack
then x is equal to pop of stack
if x is less than top of stack
then x is equal to pop of stack
else x is greate than top of stack
drop (pop) the stack
if x is less than top of stack
then x is equal to pop of stack
- Q6 Let A be an array of size n ≥ 2 containing integers from 1 to n − 1 inclusive, one of which is repeated. Describe an algorithm for finding the integer in A that is repeated.
Solution
int x = A[0];
for (int i =1 ; i<A.length ;i++){
if (x == A[i]){
break; // found x
}
x = A[i]
}
- Q7 Give an algorithm for finding the second-to-last node in a singly linked list in which the last node is indicated by a null next reference.
Solution
public E secondToLast() {
if (isEmpty() || size < 2 )
return null;
while (head.getNext.getNext != Null)
head = head.getNext();
return head;
}
- Q8 Calculate the Big(o) for the following code:
public static int example5(int[ ] first, int[ ] second) { // assume equal-length arrays
int n = first.length, count = 0; // T1 = a
for (int i=0; i < n; i++) { // T2 = n * T3 = n * (T4 + T5 + T8) = b*n + c*n^3 + d * n
int total = 0; // T4 = b
for (int j=0; j < n; j++) // T5 = n * T6 = n * c * n == c * n^2
for (int k=0; k <= j; k++) // T6 = n * T7 = c * n
total += first[k]; // T7 = c
if (second[i] == total) count++; // T8 = d
}
return count;
//Big(o) = O(n^3)
}