Week 7: Binary Search Trees, Sets (ADT) and Maps (ADT)

• Objectives
• Trees
  • Tree Glossary
  • Synonyms
  • Violating Tree Structure
• Binary Search Trees (BST)
  • Motivation
  • Intuition
  • Design and Implementation: Using Linked Structures
  • Operations
    • Is Empty
    • Is Leaf
    • Size
    • Insertion
    • Search
    • BST Traversal
    • Traversal: In-order
    • Traversal: Pre-order
    • Traversal: Post-order
    • Traversal: Breadth-first
    • Clear the whole tree
    • Removal of element
• Asbtract Data Types Built Upon BST
  • Set
    • Operations
  • Map
    • Implementing a Dictionary (i.e Map) Using BST

Objectives

1. Learn about graph structures in a glimpse
2. Specializing a graph into trees
3. Specializing trees into binary trees
4. Specializing trees into binary search trees (BST)
5. Implementing set (ADT) using BST

Trees

In previous weeks, we have learned about:

• Arrays
• Linked Lists
• Queues
• Stacks

These structures are conceptually linear structures. However, there also exist very important kind of structures that are inherently non-linear (e.g trees and graphs). Trees are special case of graphs, where nodes and edges (links) do not form a cycle.

Tree Glossary

• Root: is the top node in the tree.
• Child: any node that is emerged from an upper node.
• Parent/Internal Node: node with at least one child.
• Siblings: nodes sharing the same parent.
• Leaf: node with no children.
• Edge: the link between two nodes (i.e a parent and its child).
• Path: the sequence of links and nodes to reach from one node to a descedant.
• Height of node: the number of links between a node and the furthest leaf.
• Depth of node: the number of links between a node and the root.

Synonyms

• Node = Vertex = Point
• Edge = Link = Arc

Violating Tree Structure

wikipedia

The following structures are not trees:

Graphs that are not trees	Why?
	cycle B→C→E→D→B. B has more than one parent (inbound edge).
	undirected cycle 1-2-4-3. 4 has more than one parent (inbound edge).
	two non-connected parts, A→B and C→D→E. There is more than one root.

Binary Search Trees (BST)

Binary trees is a special case of trees where each node can have at most 2 children. Also, these children are named: left child or right child. A very useful specialization of binary trees is binary search tree (BST) where nodes are conventionally ordered in a certain manner. By convention, the \(\text{left children} < \text{parent} < \text{right children}\), and this rule propagates recursively across the tree.

A binary search tree (BST)

Specialization from graph->tree->BT->BST

Motivation

Efficient search & insertion/deletion in logarithmic time $O(\log(n))$

• Arrays:
  • (+) efficient search on sorted arrays $O(\log(n))$,
  • (-) ineffiecient insertion/deletion $O(n)$.
• Linked lists:
  • (-) inefficient search $O(n)$,
  • (+) efficient insertion/deletion $O(1)$.

Intuition

• Tree combines the advantages of arrays and linked lists.
• The nature of BST (i.e being ordered) makes it potential for extensive applications. For example, implementing set (ADT).

Design and Implementation: Using Linked Structures

Tree structure allows us to use recursive routines to implement the basic operations. Think of each node in a tree as a separate standalone tree. Trees can be embedded in arrays or implemented as a linked nodes (i.e using pointers). In this tutorial, we will implement the BST using linked nodes. Any node in the tree (including the root) will be represented by the type BSTNode that has the following C++ `struct:

struct BSTNode
{
    int data;
    BSTNode *left;
    BSTNode *right;
};

Operations

Is Empty

bool isEmpty( BSTNode *tree )
{
    return tree == nullptr;
}

Is Leaf

bool isLeaf( BSTNode *tree )
{
    return tree->left == nullptr && tree->right == nullptr;
}

Size

int size( BSTNode *tree )
{
    if ( !isEmpty( tree ))
        return 1 + size( tree->left ) + size( tree->right );
    else return 0;
}

Insertion

Insertion in BST, realize recursion. Author

void insert( BSTNode *&tree, int data )
{
    if ( isEmpty( tree ))
        tree = new BSTNode{ data , nullptr , nullptr };

    else
    {
        if ( data < tree->data )
            insert( tree->left, data );

        else insert( tree->right, data );
    }
}

Search

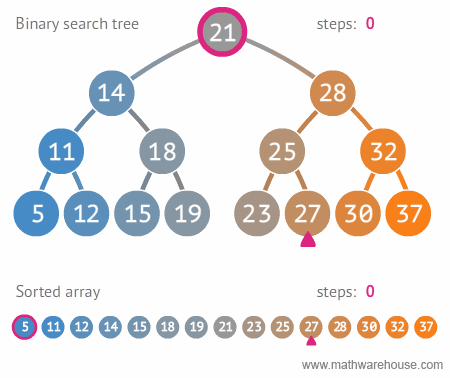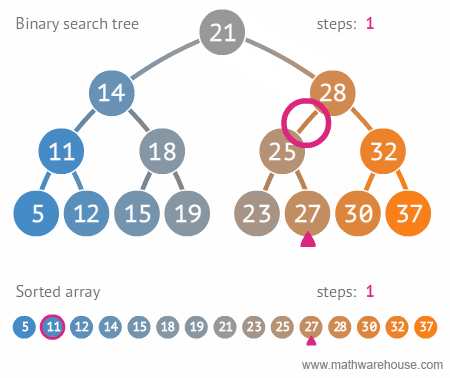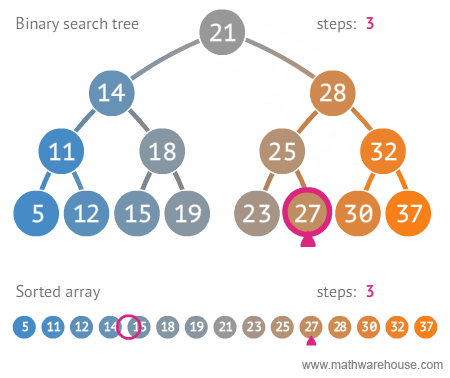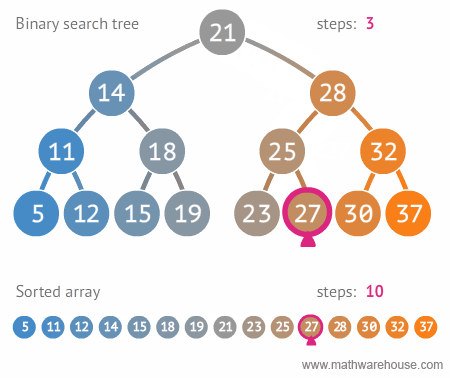Search in BST, realize recursion. Author

bool find( BSTNode *tree, int data )
{
    if ( isEmpty( tree ))
        return false;
    else
    {
        if ( data == tree->data )
            return true;

        else if ( data < tree->data )
            return find( tree->left , data );

        else return find( tree->right , data );
    }
}

BST Traversal

Pre- In- Post-order Traversals
Made using: Khan Academy Computer Science

Traversal: In-order

In-order Traversal in BST, realize recursion. Source

void inorder( BSTNode *tree )
{
    if( tree )
    {
        inorder( tree->left );
        std::cout << "[" << tree->data << "]";
        inorder( tree->right );
    }
}

Traversal: Pre-order

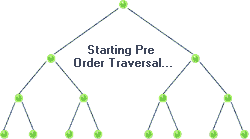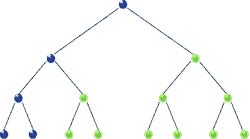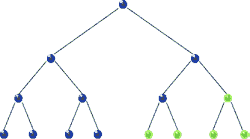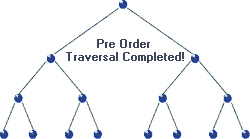Pre-order Traversal in BST, realize recursion. Source

void preorder( BSTNode *tree )
{
    if( tree )
    {
        std::cout << "[" << tree->data << "]";
        preorder( tree->left );
        preorder( tree->right );
    }
}

Traversal: Post-order

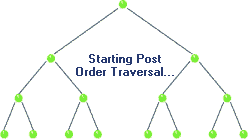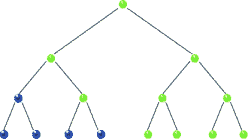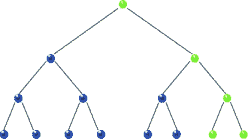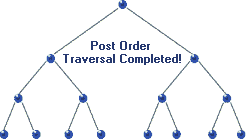Post-order Traversal in BST, realize recursion. Source

void postorder( BSTNode *tree )
{
    if( tree )
    {
        postorder( tree->left );
        postorder( tree->right );
        std::cout << "[" << tree->data << "]";
    }
}

Traversal: Breadth-first

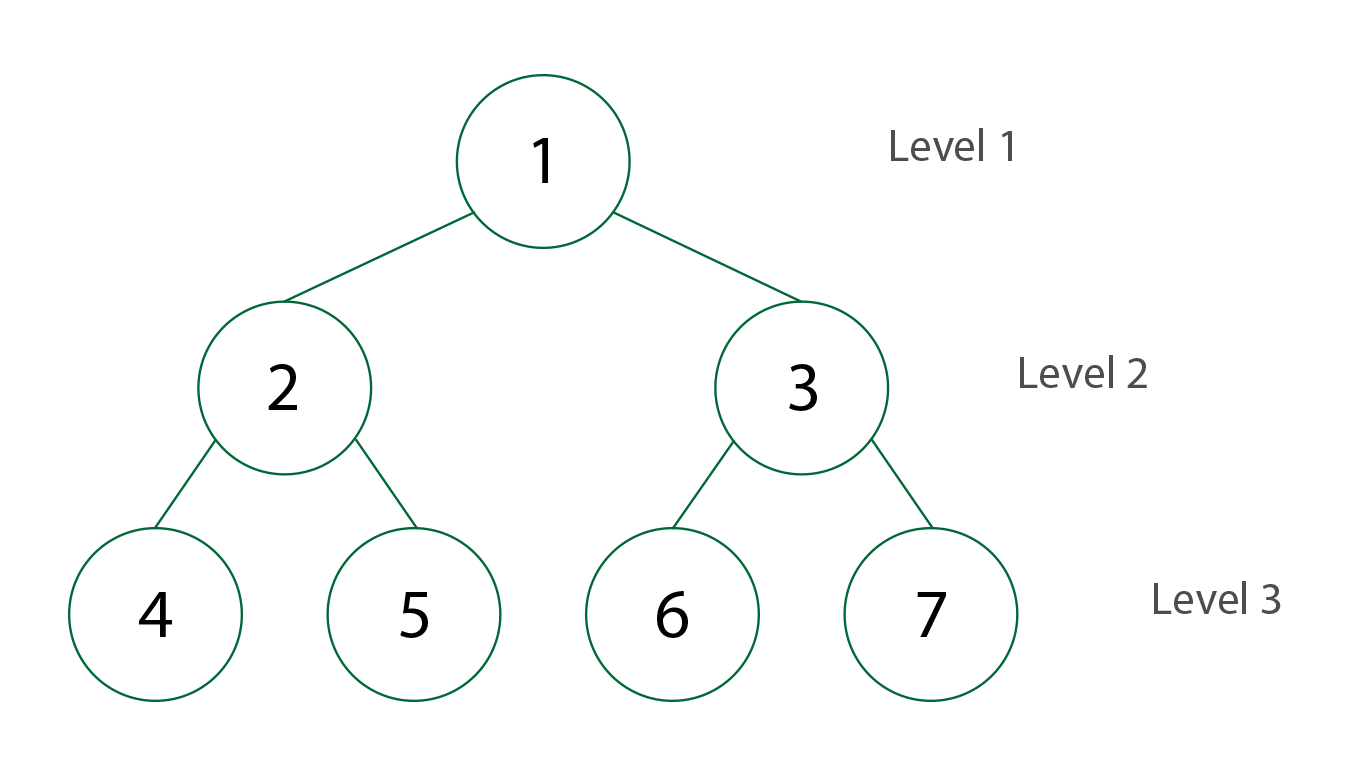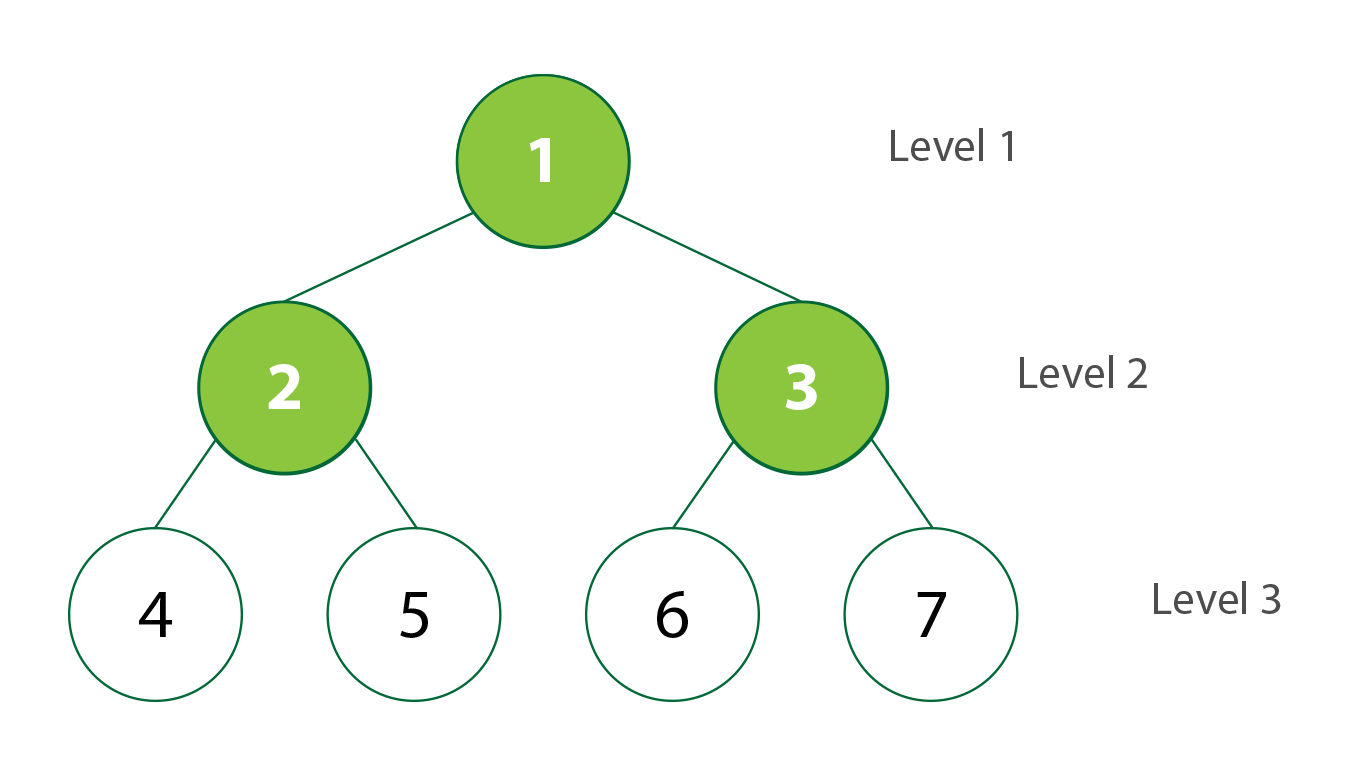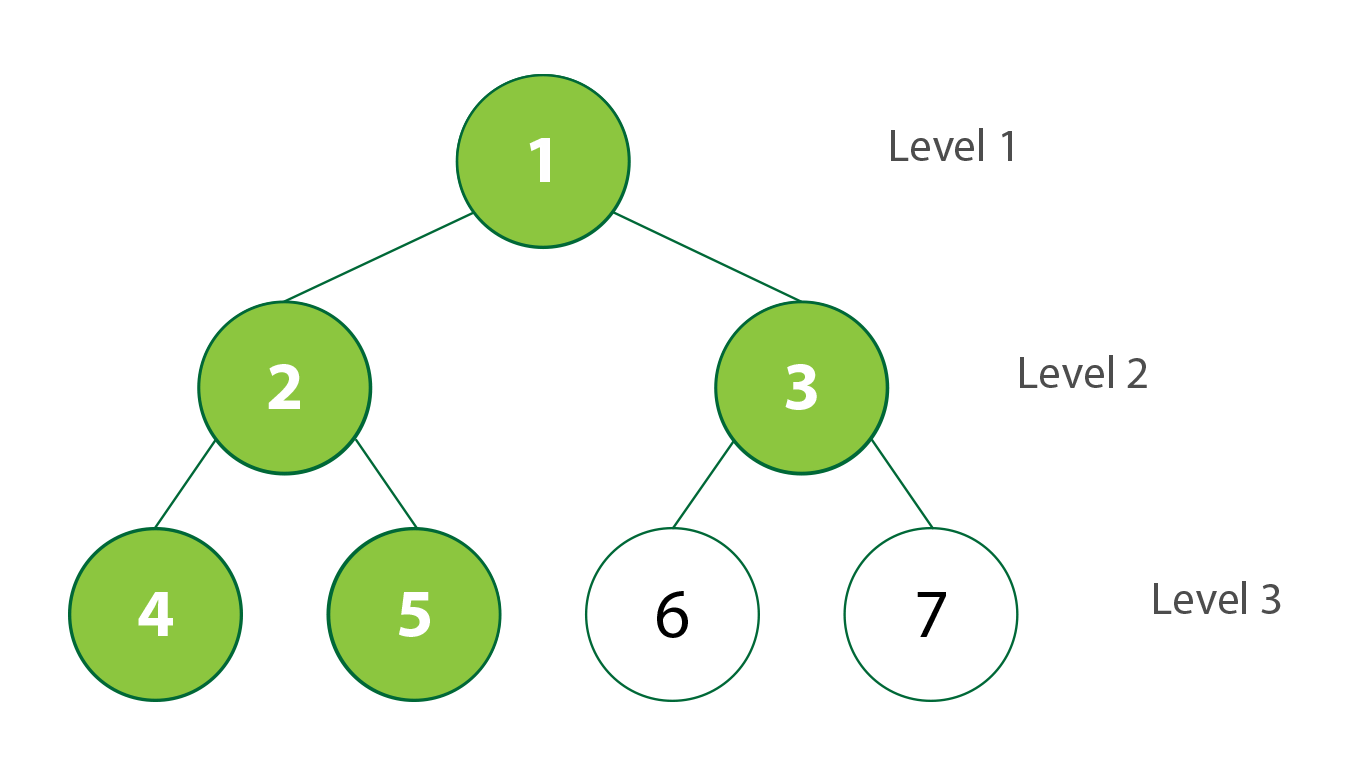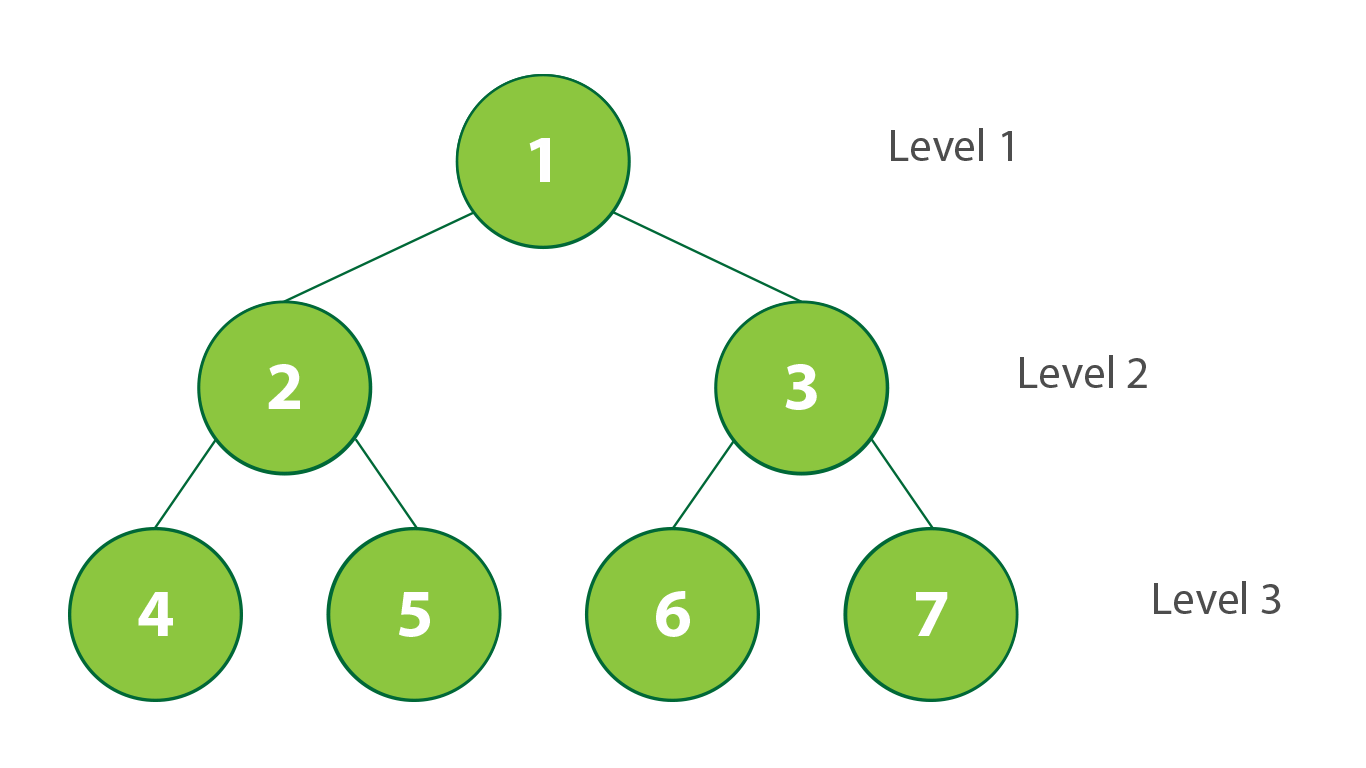Breadth-first Traversal in BST. Created by Stephanie Wong

Clear the whole tree

void clear( BSTNode *&tree )
{
    if ( !isEmpty( tree ))
    {
        clear( tree->left );
        clear( tree->right );
        delete tree;
        tree = nullptr;
    }
}

Removal of element

Case	Action	Example
Case I: Node to be removed has no children	Simplest case. Algorithm sets corresponding link of the parent to NULL and deletes the node	remove( tree , -4 )
Case II: Node to be removed has one child	It this case, node is cut from the tree and algorithm links single child (with it’s subtree) directly to the parent of the removed node	remove( tree , 18 )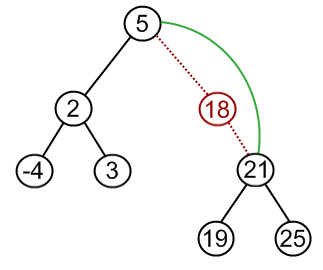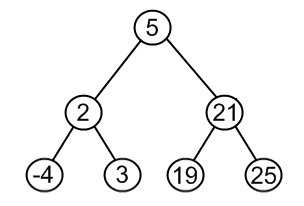
Case III: Node to be removed has two children	This is the most complex case. To solve it, (1) find a minimum value in the right subtree; (2) replace value of the node to be removed with found minimum. Now, right subtree contains a duplicate! (3) apply remove to the right subtree to remove a duplicate.
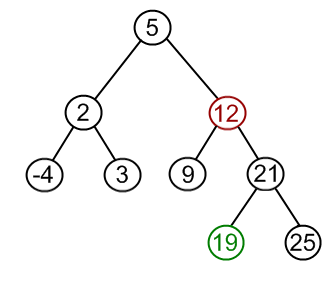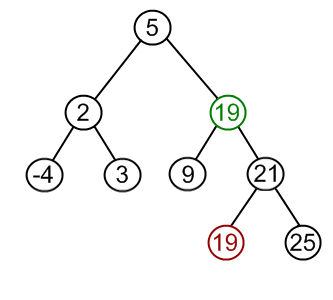Source: http://www.algolist.net/

void remove( BSTNode *&tree, int data )
{
    if ( isEmpty( tree )) return;

    if ( data == tree->data )
    {
        if ( !isEmpty( tree->left ) && !isEmpty( tree->right ))
        {
            BSTNode *minRight = minNode( tree->right );
            tree->data = minRight->data;
            remove( tree->right, minRight->data );
        } else
        {
            BSTNode *discard = tree;

            if ( isLeaf( tree ))
                tree = nullptr;
            else if ( !isEmpty( tree->left ))
                tree = tree->left;
            else
                tree = tree->right;

            delete discard;
        }

    } else if ( data < tree->data )
        remove( tree->left, data );
    else remove( tree->right, data );
}

Asbtract Data Types Built Upon BST

Set

We can harness the sorted property of BST to make efficient insertions and removals. Also, with a slight modification to the insert function, we can make this function only insert unique values, hence our new set (ADT) will always contain unique values.

Operations

• isEmpty: same as BST
• size: same as BST
• contains: same as find of BST
• remove: same as BST
• insert: slight modification of bst::insert, such that insertion is done when the element isn’t a duplicate of existing element, possible implementation:
  1. use contains to check if element doesn’t already exist,
  2. then, if the condition holds, use bst::insert, otherwise, do nothing.
• union: given two sets $S_1$ and $S_2$ make a new data structure $S_3 = S_1 \cup S_2$, possible implementation:
  1. make an empty set S3,
  2. iterate over elements of S1 inserting each element to S3, and similarly for S2.
• intersect: given two sets $S_1$ and $S_2$ make a new data structure $S_3 = S_1 \cap S_2$, possible implementation:
  1. make an empty set S3,
  2. iterate over elements of S1 inserting each element that also exists in S2 into S3.
• equals: given two sets $S_1$ and $S_2$, check the equality of the two sets, possible implementation:
  1. first, check that $S_1$ and $S_2$ sizes are equal,
  2. then, iterating in-order in parallel in both $S_1$ and $S_2$ to validate the equality of traversed elements.

Map

Synonyms: Associative containers, dictionary, symbol table.

A map is a collection of searchable key-value pairs, where each key has a value.

Example 1, we can have a map representing count of words in a page or textbook, so the key here is the word, while the value is the count of this word.

Example 2, for the function that counts characters in DNA:

int countCharacter( std::string dna, char query )
    {
        int count = 0;
        for ( int i = 0; i < dna.size(); ++i)
        {
            if ( query == dna[i] )
                ++count;
        }
        return count;
}
int main( int argc, char **argv )
{
    if( argc == 2 )
    {
        std::string dna = getDNA( argv[1] );

        int countA = countCharacter( dna , 'A');
        int countC = countCharacter( dna , 'C');
        int countG = countCharacter( dna , 'G');
        int countT = countCharacter( dna , 'T');

        std::cout << "A:" << countA << std::endl
                  << "C:" << countC << std::endl
                  << "G:" << countG << std::endl
                  << "T:" << countT << std::endl;
    }

    return 0;
}

This function was called four times (i.e to count A, C, G, and T). However, by using map data structure we can run this function to count all characters in a single run!

int main( int argc, char **argv )
{
    if( argc == 2 )
    {
        std::string dna = getDNA( argv[1] );

        char_map::CharMap dnaCounter = char_map::create();

        for( int i = 0 ; i < dna.size() ; ++i )
            map::value( dnaCounter , dna[i] )++;

        char_map::printAll( dnaCounter );
    }

    return 0;
}

Implementing a Dictionary (i.e Map) Using BST

Map implementation using BST would be as easy as implementing a set using the concrete routines of BST.

1. create: returns empty dictionary.
2. isEmpty: checks if dictionary is empty.
3. size: returns the size of the dictionary.
4. insert: inserts new key to the dictionary.
5. remove: remove an element by its key.
6. at: returns a reference to the value associated with a given dictionary. Crashes if the key is not found.
7. value: returns a reference to the value associated with a given key. If key not found, then insert a new key with the given key then returns a reference to the newly created value.
8. contains: checks if a key exists in the dictionary.

struct MapNode
{
    std::string key;
    int value;
    MapNode *left;
    MapNode *right;
};