Week 10: Merge and Quick Sorting, more on Dijkstra, and the Final Project

• Divide and Conquer Strategy: The Merge Sorting
  • Complexity Analysis
  • Implementation
    • Divide and Conquer
    • Combine the small solutions
  • John Von Neumann
• Divide and Conquer Strategy: The Quick Sorting
  • QuickSort: Implementation
• The Shortest Path (TSP) Problem using Dijkstra’s
  • Dijkstra: Exercise
  • Edsger Wybe Dijkstra
• Next Week: Workshop
  • Prerequisites

Divide and Conquer Strategy: The Merge Sorting

We can employ the divide and conquer principle in sorting arrays. Divide and Conquer principle basically divides the big problem into smaller sub-problems an attempts to exploit the solutions of smaller problems to obtain the solution of the big problem.

Merge Sort animated
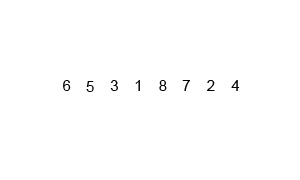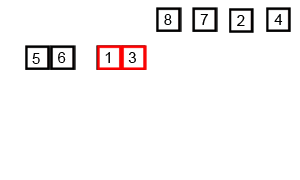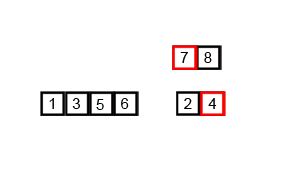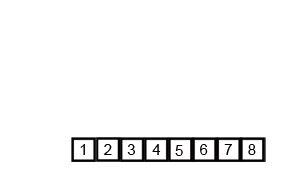Creative Commons

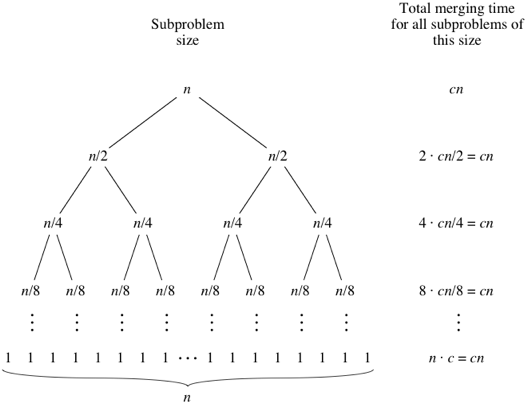
Complexity Analysis

Merge Sort Analysis via diagram
CC-BY-NC-SA

For advanced details, see Analysis of merge sort | Khan Academy.

Implementation

Divide and Conquer

void mergeSort( std::vector< double > &a , int low, int high)
{
	if (low < high)
	{
		int mid=(low+high)/2;
		// Split the data into two half.
		mergeSort(a, low, mid);
		mergeSort(a, mid+1, high);
 
		// Merge them to get sorted output.
		merge(a, low, mid, high);
	}
}

Combine the small solutions

void merge( std::vector< double > &a , int low, int mid , int high )
{
    int n1 = mid - low + 1;
    int n2 =  high - mid;
 
    std::queue<double> left, right;
    
    for (int i = 0; i < n1; i++)
        left.push( a[low + i] );
    for (int i = 0; i < n2; i++)
        right.push( a[mid + 1 + i]);
    
    int offset = low;
    while( !left.empty() && !right.empty())
    {
        if( left.front() < right.front())
        {
            a[ offset ] = left.front();
            left.pop();
        }
        else
        {
            a[ offset ] = right.front();
            right.pop();
        }
        ++offset;
    }

    while( !left.empty())
    {
        a[ offset++ ] = left.front();
        left.pop();
    }
    while( !right.empty())
    {
        a[ offset++ ] = right.front();
        right.pop();
    }
}

John Von Neumann

John Von Neumann (1903-1957)

Neumann has made tremendous scientific contributions in the modern history. His contributions were mainly foundational in several mathematical fields, such as:

• Game Theory
• Quantum Mechanics
• Ergodic Theory
• Computer Science

He also worked in the Manhattan Project.

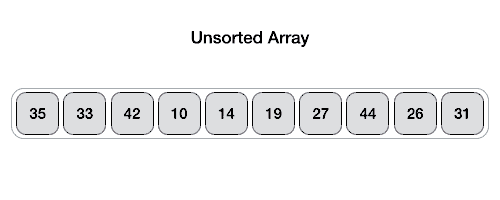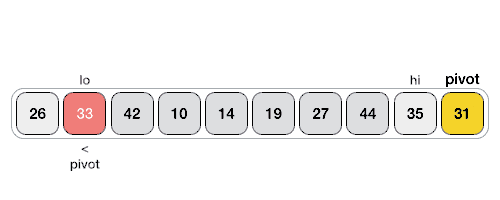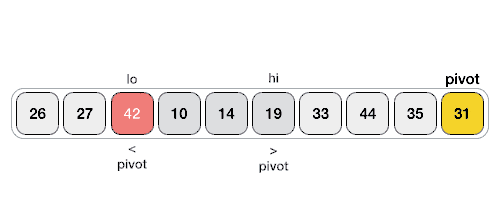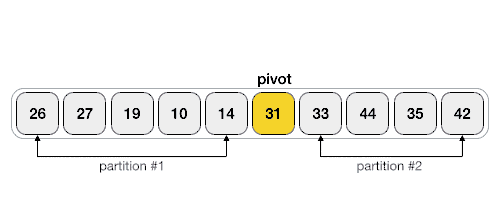
Divide and Conquer Strategy: The Quick Sorting

Like Merge Sort, Quick Sort utilizes divide and conquer strategy; it divides the big problems into smaller sub-problems.

Quick Sort animated
source

Pivot selection:

1. first element
2. last element
3. median
4. random

QuickSort: Implementation

void quickSort( std::vector< double > &a, int low, int high)
{
    if (low < high)
    {
        int pIdx = partition(a, low, high);

        if (low < pIdx)
            quickSort(a, low, pIdx - 1); // Before pi
        if (high > pIdx)
            quickSort(a, pIdx + 1, high); // After pi
    }
}

int partition( std::vector< double > &a, int low, int high )
{
    int pivot = a[low];

    int i = low + 1, j = high;

    while (i <= j)
    {
        while (i <= j && a[i] < pivot)
            ++i;
        while (i <= j && a[j] > pivot)
            --j;
        if (i <= j)
            std::swap(a[i++], a[j--]);
    }
    std::swap( a[--i] , a[low] );
    return i;
}

The source code:

git clone git@github.com:sbme-tutorials/sbe201-merge.git

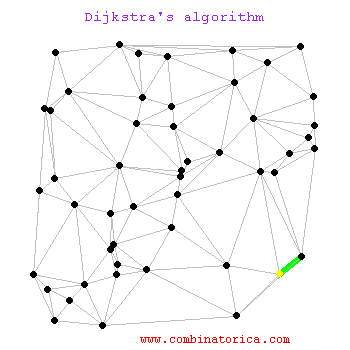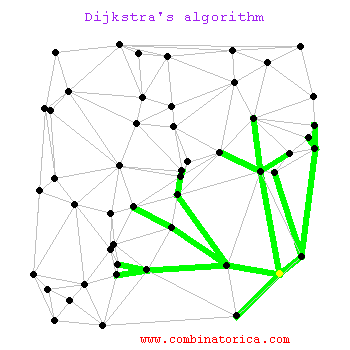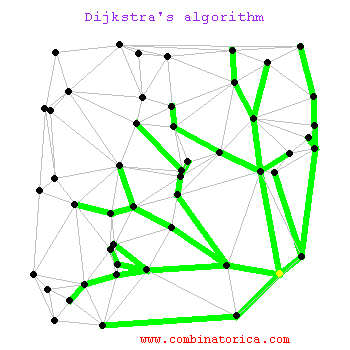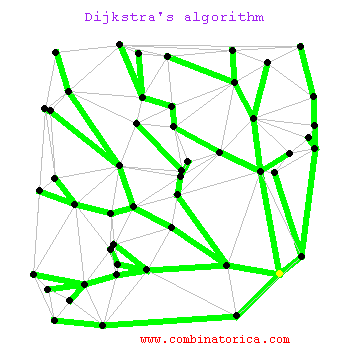
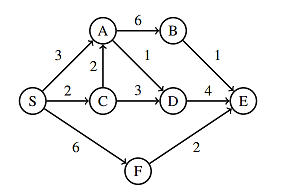
The Shortest Path (TSP) Problem using Dijkstra’s

Dijkstra animated
source

Read Finding The Shortest Path, With A Little Help From Dijkstra

Dijkstra: Exercise

Edsger Wybe Dijkstra

Edsger Wybe Dijkstra (1930-2002)

Simplicity is prerequisites for reliability — Dijkstra

Next Week: Workshop

Prerequisites

1. Install Qt and QtCreator.
2. Install CMake.
3. Coursera Account.
4. Install Jekyll.
5. Install Latex and TexMaker.