Images as Arrays

RGB Images

For RGB images, each pixel is composed of three channels, namely: red, green, and blue.

Binary Images and Scaler Images

  • A pixel in a binary image is either 0 or 1.
  • A pixel in a scaler image is composed of a single channel with scaler value.
    • Example: 256-grayscale images.

Converting from RGB to Grayscale

For each RGB pixel, we compute a combination of the three values into single value. In literature, using a combination of \(\big[0.299, 0.587, 0.114\big]\) is extensively used.

\[I = \big[0.299, 0.587, 0.114\big] . \big[R, G, B\big]^T\] 
def rgb2gray(rgb_image):
    return np.dot(rgb_image[...,:3], [0.299, 0.587, 0.114])

Converting from Grayscale to Binary Image

We can binarize an image by using a threshold value, such that pixel value is 1 if \(I > \text{threshold}\) and 0 otherwise.

def binarize( gray_image , threshold ):
    threshold = np.max( gray_image ) * threshold
    return 1 * ( gray_image > threshold )

Mean and Variance

print( np.mean( image ))

print( np.std( image ))

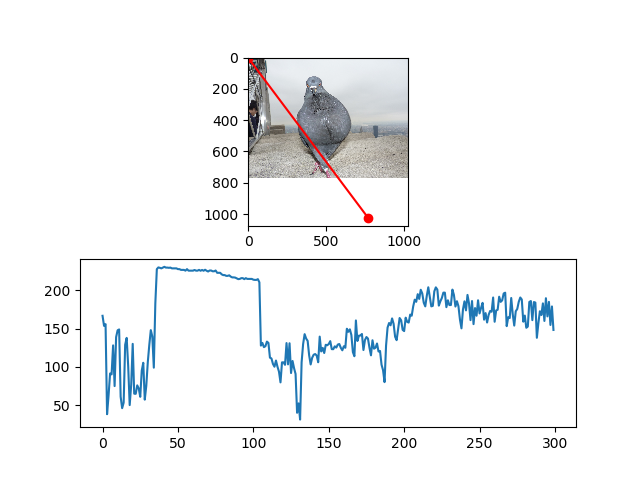
Profiles

x0 = 0
x1 = gray_image.shape[0] - 1
y0 = 0
y1 = gray_image.shape[1] - 1

x, y = np.linspace(x0, x1, 300), np.linspace(y0, y1, 300)
profile = gray_image[x.astype(np.int), y.astype(np.int)]

#-- Plot...
fig, axes = plt.subplots(nrows=2)
axes[0].imshow(gray_image)
axes[0].plot([x0, x1], [y0, y1], 'ro-')
axes[0].axis('image')

axes[1].plot(profile)

plt.show()

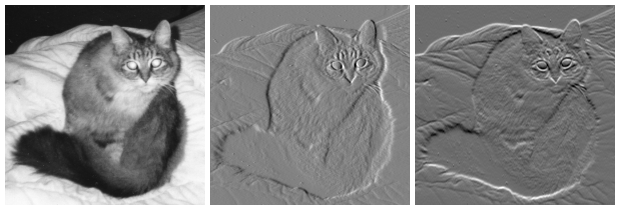
Edges

In images, we are always interested to define the boundaries of objects existing in an image, and separating it from background. Edge detection is fundamental step in many Computer Vision pipelines. The simplest form of edge detection is applying mathematical differentiation on image data. Since we work with digital pixels, we will apply difference equations.

First-Order Derivatives

\[\nabla f=\begin{bmatrix} g_{x} \\ g_{y} \end{bmatrix} = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}\]

where:

\(\textstyle\frac{\partial f}{\partial x}\) is the derivative with respect to x (gradient in the x direction)

\(\textstyle\frac{\partial f}{\partial y}\) is the derivative with respect to y (gradient in the y direction).

Computer Vision Opportunities

Internship at Affectiva

A very interesting talk by Rana Elkaliouby about Affectiva:

360imaging in Egypt

An intuitive and easy to use treatment planning software for accurate and predictable planning of implant cases.

Website

  • Planned Dental Surgeries.
  • They demand highly skilled C++ developers.
  • Computer Vision background is a plus
  • They offer opportunities through Wuzzuf.

Resources

Week 1: Demo and Lab Source Files

$ git clone https://github.com/sbme-tutorials/sbe401-week2-demo.git