Week 6-b: Queues
Queue
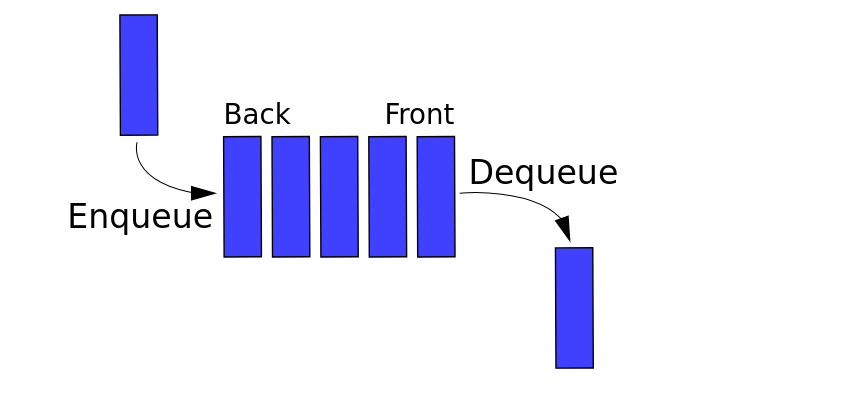
Another fundamental data structure is the queue. It is a close “cousin” of the stack, but a queue is a collection of objects that are inserted and removed according to the first-in, first-out (FIFO) principle. That is, elements can be inserted at any time, but only the element that has been in the queue the longest can be next removed.
- Abstract Data Type (ADT),
- Many implementations (e.g arrays and linked lists)
- Queue behaviour == FIFO (first in, first out).
Essential Operations
- enqueue: Adds element e to the back of queue.
- dequeue: Removes and returns the first element from the queue.
Non-Essential Operations
- first: Returns the first element of the queue, without removing it.
- size: Returns the number of elements in the queue.
- isEmpty: Returns a boolean indicating whether the queue is empty.
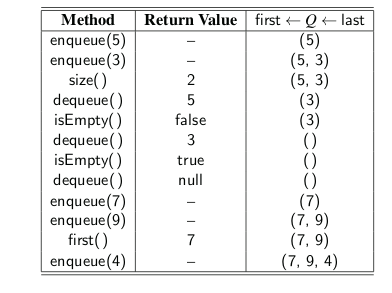
A Queue Interface in Java
The queue abstract data type defines a collection that keeps objects in a sequence, where element access and deletion are restricted to the first element in the queue, and element insertion is restricted to the back of the sequence. This restriction enforces the rule that items are inserted and deleted in a queue accord- ing to the first-in, first-out (FIFO) principle.
public interface Queue<E> {
/** Returns the number of elements in the queue. */
int size();
/** Tests whether the queue is empty. */
boolean isEmpty();
/** Inserts an element at the rear of the queue. */
void enqueue(E e);
/**
* Returns, but does not remove, the first element of the queue (null if empty).
*/
E first();
/** Removes and returns the first element of the queue (null if empty). */
E dequeue();
}
Array-Based Queue Implementation
public class ArrayQueue<E> implements Queue<E> {
public static final int CAPACITY = 1000; // default array capacity
private E[] data; // generic array used for storage
private int front = 0; // index of the front element
private int rear = 0; // current number of elements
public ArrayQueue() {
this(CAPACITY);
}
public ArrayQueue(int capacity) {
data = (E[]) new Object[capacity];
}
@Override
public int size() {
return rear;
}
@Override
public boolean isEmpty() {
return rear == 0;
}
@Override
public void enqueue(E e) {
if (rear == data.length)
throw new IllegalStateException("Queue is full");
int avail = (front + rear) % data.length;
data[avail] = e;
rear++;
}
@Override
public E first() {
if (isEmpty())
return null;
return data[front];
}
@Override
public E dequeue() {
if (isEmpty())
return null;
E answer = data[front];
data[front] = null;
front = (front + 1) % data.length;
rear--;
return answer;
}
public static void main(String[] args) {
Queue<Integer> Q = new ArrayQueue<>();
Q.enqueue(5);
Q.enqueue(3);
System.out.println(Q.size());
System.out.println(Q.dequeue());
System.out.println(Q.isEmpty());
System.out.println(Q.dequeue());
System.out.println(Q.isEmpty());
System.out.println(Q.dequeue());
Q.enqueue(7);
Q.enqueue(9);
System.out.println(Q.first());
Q.enqueue(4);
System.out.println(Q.first());
Q.enqueue(6);
Q.enqueue(8);
System.out.println(Q.first());
}
}
Implementing a Queue with a Singly Linked List
As we did for the stack ADT, we can easily adapt a singly linked list to imple- ment the queue ADT while supporting worst-case O(1)-time for all operations, and without any artificial limit on the capacity. The natural orientation for a queue is to align the front of the queue with the front of the list, and the back of the queue with the tail of the list, because the only update operation that singly linked lists support at the back end is an insertion.
public class LinkedQueue<E> implements Queue<E> {
private SinglyLinkedList<E> data = new SinglyLinkedList<>(); // an empty list
public LinkedQueue() {
}
@Override
public int size() {
return data.size();
}
@Override
public boolean isEmpty() {
return data.isEmpty();
}
@Override
public void enqueue(E e) {
data.addLast(e);
}
@Override
public E first() {
return data.first();
}
@Override
public E dequeue() {
return data.removeFirst();
}
public static void main(String[] args) {
Queue<Integer> Q = new ArrayQueue<>();
Q.enqueue(5);
Q.enqueue(3);
System.out.println(Q.size());
System.out.println(Q.dequeue());
System.out.println(Q.isEmpty());
System.out.println(Q.dequeue());
System.out.println(Q.isEmpty());
System.out.println(Q.dequeue());
Q.enqueue(7);
Q.enqueue(9);
System.out.println(Q.first());
Q.enqueue(4);
System.out.println(Q.first());
Q.enqueue(6);
Q.enqueue(8);
System.out.println(Q.first());
}
}