Big O Notation for Algorithm Analysis

What is an Algorithm

According to Donald Knuth, the word algorithm is derived from the name “al-Khowârizmı̂,” a ninth-century Persian mathematician.

In programming,

  • algorithm is a function with some logic.
  • Very general term.
  • The meanArray function is an *algorithm
  • Similary, varianceArray, minArray, maxArray, factorial, and power.

We are .red[concerned] about the function running time w.r.t input size n.

Estimating the running time $T(n)$

  • $T(n)$ is the running time function.
  • $n$ is size of the data structure.
  • printing array of size 10 takes less time than array of size 1000 ($T(10) < T(1000)$)

Example

void printArray( double[] array, int size ) // n = size
{
    for( int i = 0; i < size; ++i ) 
    {
        system.out.print(array[i]); // T1(n) = axn
        system.out.print(" "); // T2(n) = bxn
    }
    system.out.print("\n"); // T3(n) = c
}

$T(n) = T_1 + T_2 + T_3 = an + bn + c= c + (a+b)n $ (:thinking: linear)

Alternatively, factor out $n$

void printArray( double[] array, int size ) // n = size
{
    for( int i = 0; i < size; ++i ) // T1(n) = n * ( T2 + T3 )
    {
        system.out.print(array[i]); // T2(n) = a
        system.out.print(" "); // T3(n) = b
    }
    system.out.print("\n"); // T4(n) = c
}

$ T(n) = c + n ( T_3 + T_4 ) = c + (a+b)n $ (:thinking: linear)

with slight modification in code (no change in logic)..

void printArray( double[] array, int size ) // n = size
{
    for( int i = 0; i < size; ++i ) // T1(n) = n * ( T2 )
    {
        system.out.print(array[i] + " "); // T2(n) = d
    }
    system.out.print("\n"); // T4(n) = e
}

$T(n) = T1 + T4 = e + n ( T4 ) = e + dn$

  • Conclusion: $T(n)$ is not reliable estimate!
  • But $T(n)$ is still linear!

Other drawbacks of relying on $T(n)$

consider the following program:

public void printArray( double[] array, int size ) {
    for( int i = 0; i < size; ++i ) 
        system.out.print(array[i] + " ");
}
public static void main() {
    double a[] = {1.2, 1.3, -1.0, 0.4};
    printArray(a, 4);
}

Estimating the running time of an algorithm by $T(n)$ is unrealistic because the running time will vary:

  1. from platform to another (e.g Core i3 vs Core i9).
  2. from compiler to another (e.g GCC vs Clang vs MSVC).

Even if used the same compiler and platform, it may change from time to time (e.g summer vs. winter)

Estimating the running time $T(n)$ The asymptotic running time (big O notation)

For any of the following polynomials:

  • $T_a(n) = (a+b)n + c$
  • $T_b(n) = 2n + 1$
  • $T_c(n) = dn + e$

  • $T_d(n) = 6n + 3$

  • The $n$ term will dominate the function $T(n)$ at large $n$ values.

  • So, we propose “big O notation” to capture the dominating term at large $n$ values.
  • Such that, $O(T_a(n)) = O(T_b(n)) = O(T_c(n)) = O(T_d(n))$ = $O(n)$

The asymptotic running time (big O notation)

Quadratic Performance

Consider the following function inefficient varianceArray

double meanArray( double *array, int size){.....} // O(an + b) = O(n)
double varianceArray( double *array, int size ) // n = size
{
    double sum = 0 ; // O(1)
    for( int i = 0; i < size ; ++i )  // O(n^2)
    {
        double diff = meanArray( array, size ) - array[i]; // O(n)
        sum = sum + diff * diff ; // O(1)
    }
    return sum / size; // O(1)
}

$ O(T(n)) = O(1) + O(n^2) + O(1) = O(n^2) $

Can we do better?

Consider the following function optimized varianceArray

double meanArray( double[] array, int size){.....} // O(an + b) = O(n)
double varianceArray( double[] array, int size ) // n = size
{
    double sum = 0 ; // O(1)
    for( int i = 0; i < size ; ++i )  // O(n^2)
    {
        double diff = meanArray( array, size ) - array[i]; // O(n)
        sum = sum + diff * diff ; // O(1)
    }
    return sum / size; // O(1)
}

$ O(T(n)) = O(1) + O(n) + O(n) + O(1) = O(n) $

$O(n)$ is better than $O(n^2)$

Constant Performance

double arrayBack( double[] array, int size ) // n = size
{
    double last = array[ size - 2 ]; // O(1)
    return last; // O(1)
}
\[O( T(n) ) = O(1) + O(1) = O(1)\]

Note that:

$O(12)$ = $O(9 + log(3))$ = $O(1)$

Exercise: Estimate the $O(f(n))$

$f(n)$ dominant term $O(f(n))$
$2n + 3n^3 + 100$    
$11n + 2^n + 0.2n^3$    
$\log_2(n) + 5n$    
$a(1+cos(2\pi n)) + b\log_2(n) + cn$    
$n\log_2(n) + n^{1.5}$    

Exercise (Solution): Estimate the $O(f(n))$

$f(n)$ dominant term $O(f(n))$
$2n + 3n^3 + 100$ $3n^3$ $O(n^3)$
$11n + 2^n + n^3$ $2^n$ $O(2^n)$
$a(1+cos(2\pi n)) + b\log_2(n) + cn$ $cn$ $O(n)$
$n\log_2(n) + n^{1.5} $ +:octocat: +:octocat:

To find which is dominant for large $n$:

\[\lim_{n\to\infty} \frac{nlog_2(n)}{n^{1.5}} = 0 \text{ or } \infty\]

hint: :shipit: use l’hopital

Exercise: predict running time in seconds using small measurement

double meanArray(double[] array, int size){.....} // O(n)
double varianceArray( double[] array, int size ) { // n = size
    double sum = 0 ; // O(1)
    for( int i = 0; i < size ; ++i ) { // O(??)
        double diff = meanArray( array, size ) - array[i]; // O(n) 
        sum = sum + diff * diff ; // O(1)
    }
    return sum / size; // O(1)
}
How to approximately estimate the function varianceArray running time for $n=1000000$, i.e array of 1-million element
Givens
  • The function has complexity of $ O(n^2) $.
  • The function executed in 2 microseconds when $n=2000$.
Solution

$\frac{T(n_1)}{T(n_2)} \approx \frac{n_1^2}{n_2^2}$

$T(1000000) \approx \left( \frac{1000000}{2000} \right)^2 T(2000) = 250000 \times 2$

$T(1000000) \approx 500000 = 0.5 \text{ seconds}$

Common asymptotic functions

{Orders of common functions}

Sorting Algorithms (1)

Problem given a collection of n elements, it is required to sort the elements in ascending order.

  • Example the following arbitrary array:
1 9 4 7 3
  • After applying sorting in ascending order will result as:
1 3 4 7 9

Bubble Sort

Visualized Bubble Sort 1

Visualized Bubble Sort 2

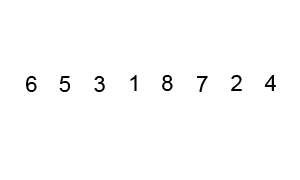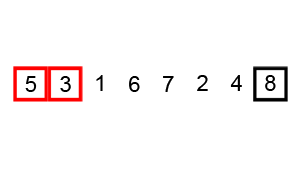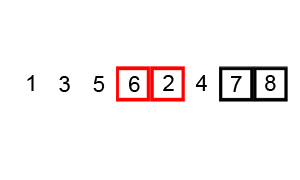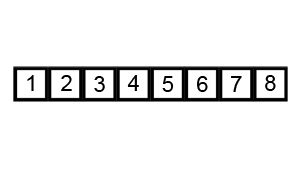
Credits: CC BY-SA 3.0

Implementation

#include <algorithm>
// A function to implement bubble sort
void bubbleSort( double[] array, int size )
{
    for ( int i = 0; i < size-1; i++ )
    {
        for ( int j = 0; j < size-1; j++ )
        {
            if ( array[j] > array[j+1])
                swap( array[j] , array[j+1] );
        }
    }
}

Time Complexity (Big O notation) Analysis

void bubbleSort(  double[] array, int size )
{
    for ( int i = 0; i < size-1; i++ ) // T1 = n * T2
    {
        for ( int j = 0; j < size-1; j++ ) // T2 = n * T3
        {
            if ( array[j] > arr[j+1] ) // T3 = a
                swap( array[j] , array[j+1] );
        }
    }
}
\[T(n) = T_1 = n \times T_2 = n \times n = an^2\] \[O(T(n)) = O(n^2)\]

Selection Sort

credits: GNU license

Implementation

void selectionSort( double[] array, int size )
{
    // One by one move boundary of unsorted subarray
    for (int i = 0; i < size -1; i++)
    {
        // Find the minimum element in unsorted array
        int min_idx = i;

        for (int j = i+1; j < size ; j++)
        {
            if ( array[j] < array[min_idx] )
                min_idx = j;
        }

        // Swap the found minimum element with the first element
        swap( array[min_idx] ,  array[i] );
    }
}

Complexity Analysis

void selectionSort( double[] array, int size ){
    for (int i = 0; i < size -1; i++) // T1 = n * ( T2 + T3 + T4 )
    {
        int min_idx = i; // T2 = a
        for (int j = i+1; j < size ; j++) // T3 = ???
        {
            if ( array[j] < array[min_idx] ) // b
                min_idx = j;
        }
        // Swap the found minimum element with the element i
        swap( array[min_idx] ,  array[i] ); // T4 = c
    }
}
\[T(n) = T_1 = n \times (T_2 + T_3 + T_4) = n \times( a + b\left( \frac{n+1}{2} - 1\right) + c )\] \[O(T(n)) = O(n^2)\]