Week 4 - Part1: Struct, Stacks, Linked Lists, and Queues

• Before starting: Stack as Data Structure != Stack Memory
• C++ Struct
• Functions overloading
• Stacks
  • Home Demo
  • More intuition about Stack as ADT
  • Implementing a Stack using Static Array
    • 1. The static array
    • Finally, let’s add a variable indicating the top element
    • Push
    • Front
    • Pop
    • Retrieving the size of stack
    • Asking our stack if it is empty
    • Final Code
• Linked Lists
  • Why linked lists
  • The Memory Mode: Array vs. Linked List
  • Pointers revisited
    • The last Node (back)
  • The LL Structure
  • Head (front)
  • Tail (back)
• Queues
  • Home Demo
  • More intuition about Queue as ADT
  • Biomedical Application: Queues of Biological Signals
  • Implementing Queue using LL
  • Implementing Queue using concrete array
    • 1. The circular buffer
    • Finally, let’s make two variables indicating the front and the back of our Queue
    • Making our buffer to act as a circular buffer

Before starting: Stack as Data Structure != Stack Memory

Stack as a data structure is not related to the stack memory area we learned about last weeks, and they are completely different things. So just refer to stack as a data structure by Stack, and the stack memory area by Stack memory. Make yourself a glossary on your notebook.

C++ Struct

In first week, we have walked through different primitive data types (PDTs), or the first-class citizens in the C++. However, we can make our own types, that consists of multiple members, using struct feature. Members in struct can either be primitive data types (PDT) or other structs. Let’s recall our example of rectangle::area function.

namespace rectangle
{
    double area( double w , double h )
    {
        return w * h;
    }
}

We could have made a custom type using struct, using the following syntax.

struct Rectangle
{
    double w;
    double h;
};

Rectangle is now a custom type, consists of two doubles. Think of it as a package. We can now make our rectangle::area function more simpler, or much readable using the following implementation.

#include <iostream>
namespace rectangle
{
    struct Rectangle
    {
        double w; // First member
        double h; // Second member
    }; // Don't forget a semicolon here!

    // Now this function is more readable. The input type explains itself.
    double area( Rectangle rectangle )
    {
        return rectangle.w * rectangle.h;
    }

    // If we have a pointer to Rectangle instead of a name for Rectangle
    // then we will access its members using the "->" arrow operator
    double area2( Rectangle *pRect )
    {
        return pRect->w * pRect->h;
    }
}

int main()
{
    rectangle::Rectangle rect{ 3 , 5 }; // declaration+initialization of Rectangle type!
    
    std::cout << rectangle::area( rect ) << std::endl;
    std::cout << rectangle::area2( &rect ) << std::endl;
    return 0;
}

We may also package an array (either static or dynamic) with its size, using struct

#include <iostream>

struct IntegerArray
{
    int *base;
    int size;
};


int sumArray1( int *base , int size )
{
    int sum = 0;
    for( int i = 0 ; i < size ; ++i )
    {
        sum += base[i];
    }
    return sum;
}

int sumArray2( IntegerArray array )
{
    int sum = 0;
    for( int i = 0; i < array.size ; ++i )
    {
        sum += array.base[ i ];
    }
    return sum;

    // DRY solution ==> return sumArray1( array.base , array.size );
}

int main()
{
    int *buffer = new int[10];
    IntegerArray array{ &buffer[0] , 10 }; // Initializes base and size members.
    
    std::cout << sumArray1( &buffer[0] , 10 ) << std::endl;
    
    std::cout << sumArray2( array ) << std::endl;
    
    // We still need to delete the array on the heap
    delete [] array.base;

    return 0;
}

We can also use struct to return multiple values, which is more safe and clean than using multiple references as input and mofifying our interesting results into these input references.

struct ECGArray // We could name it also DoubleArray
{
    double *samples;
    int size;
}

struct Statistics
{
    // Members can have default values after declaration of Statistic type variable.
    // So you don't need to explicitly to initialize them from outside.
    double mean = 0 ;
    double variance = 0 ;
    double min = 0;
    double max = 0;
}

// Very self-explaining function header!
Statistics analyzeECG( ECGArray ecg )
{
    Statistics analysis; // Declaration, and no need for explicit initialization now

    analysis.mean = // Some logic here
    analysis.variance = // Some logic there
    // And so on.

    return analysis;
}

Functions overloading

C++ allows you to have functions with same name, but different parameters.

For example, this is not allowed in C++:

double area( double w , double h )
{
    return w * h;
}

double area( double base , double height ) // Compiler Error
{
    return base * height / 2;
}

It becomes ambiguous now to call area(1.4,5), which area function should be called?

However, it is supported by C++ to have functions with same name, but different parameters (different types or different number of parameters).

struct Rectangle
{
    double w;
    double h;
}

double area( double d )
{
    return d * d; // square area
}

double area( double w, double h)
{
    return w * h;
}

double area( Rectangle rect )
{
    return rect.w * rect.h;
    // DRY solution ==> return area( rect.w , rect.h );
}

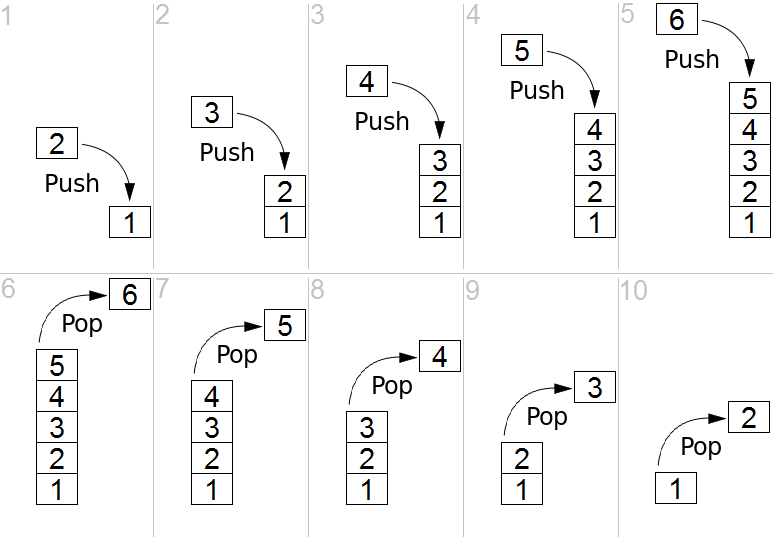
Stacks

In fact, Stack is more of behaviour of structure than being a structure itself. We can turn a regular array (either static or dynamic) into a stack with simple modification. Stack is an Abstract Data Type (ADT) they may have different implementations:

• Using arrays.
• Using linked lists (later on this note).

For both implementations, the following requirements should be satisfied in order to hava an ADT Stack (from wikipedia):

• push, which adds an element to the collection,
• pop, which removes the most recently added element that was not yet removed,
• front, which returns the most recent element in the stack.

The order in which elements come off a stack gives rise to its alternative name, LIFO (last in, first out). Additionally, a peek operation may give access to the top without modifying the stack. – Stack (Abstract Data Type).

This table should draw the boundaries between Abstract Data Types (ADT) and Concrete Data Types, and keep in mind that Abstract Data Types are built upon Concrete Data Types.

Abstract Data Type (ADT)	Possible Implementations
Stack	Array or Linked List
Queue	Array or Linked List

So again, we can turn an array into a Stack using minor modifications.

Home Demo

Open StackArray and play with the stack to realize its behaviour. This demo shows a Stack implemented with arrays.

More intuition about Stack as ADT

This video should give you an intuition about Stack as an asbtract data type (ADT).

Implementing a Stack using Static Array

As we learned earlier in this page, we have an awesome feature in C++ called struct. We can make all the stack important variable in one box. So, this box should include.

1. The static array

We need to make an array with a relatively large capacity for our stack. Let’s make a static array in our box with size 100. Size 100 is the size of the static array, which is the maximum size our Stack can have. However, initially, our Stack is empty.

// Let's make a new type for our stack with a name indicating its properties:
// 1. Our element types are integers.
// 2. The ADT is Stack
// 3. Maximum size is 100
struct IntegerStack100
{
    int buffer[ 100 ];
    int capacity = 100;
}

Finally, let’s add a variable indicating the top element

struct IntegerStack100
{
    int buffer[ 100 ];
    int top = -1;
    // Default value of top is -1 when declaring the stack.
    // -1 means our stack is empty
};

Now we have all what we need for a stack. Let’s now implement our operations

Push

When pushing a new element, we will increment the top variable, and add the new value to the array at top position.

IntegerStack100 push( IntegerStack100 stack , int newElement )
{
    ++stack.top;
    stack.buffer[ stack.top ] = newElement;
    return stack;
}

• This version passes by value then returns the new stack.
• Note that we need to return the updated IntegerStack100 because we have modified a copy, not the original object.

Alternatively, we can pass the IntegerStack100 by reference, so no need for returning the updated stack, we already modified the original stack using a reference.

void push( IntegerStack100 &stack , int newElement )
{
    ++stack.top;
    stack.buffer[ stack.top ] = newElement;
}

Front

Retrieve the first element in the stack (aka the most recent element), which is pointed to by top.

int front( IntegerStack100 &stack )
{
    return stack.buffer[ stack.top ];
}

Pop

To pop the stack, we just need to decrement the top variable.

IntegerStack100 pop( IntegerStack100 stack )
{
    --stack.top;
    return stack;
}

• This version passes by value then returns the new stack.

Alternatively, we can pass by reference and modify in-place, so no need to return the modified stack.

void pop( IntegerStack100 &stack )
{
    --stack.top;
}

Retrieving the size of stack

It is important to have an operation that returns the size of stack (its elements count).

int size( IntegerStack100 &stack )
{
    return ( stack.top + 1 ); // simple
}

Asking our stack if it is empty

We also need to a function to ask our stack if it is empty or not.

bool isEmptyStack( IntegerStack100 &stack )
{
    if( stack.top == -1 )
    {
        return true;
    }
    else
    {
        return false;
    }
}

Wouldn’t be much simpler to say:

bool isEmptyStack( IntegerStack100 &stack )
{
    return ( stack.top == -1 );
}

Final Code

Here is the final code, but we implemented if for stack of char elements instead. Releazie that there is no difference in logic.

struct CharStack1000
{
    char buffer[ 1000 ];
    int top = -1;
    // Default value of top is -1 when declaring the stack.
    // -1 means our stack is empty
};

void push( CharStack1000 &stack , char newElement )
{
    ++stack.top;
    stack.buffer[ stack.top ] = newElement;
}

char front( CharStack1000 &stack )
{
    return stack.buffer[ stack.top ];
}

void pop( CharStack1000 &stack )
{
    --stack.top;
}

int size( CharStack1000 &stack )
{
    return ( stack.top + 1 ); // simple
}

bool isEmptyStack( CharStack1000 &stack )
{
    return ( stack.top == -1 );
}

Practice yourself, and make other Stack versions of int, double, and bool. Also, make other variants of your Stack that works with dynamic arrays. In this case, the struct should hold pointer to the first element of the array.

Linked Lists

Arrays as we learned are allocated as contiguous elements in the memory (i.e a single block). In contrast, we may have our elements to be sparse in memory, but each element can see the next element. This kind of structure is called Linked List.

Why linked lists

Linked lists are very flexible in size. Our Arrays once constructed we cannot change their sizes, but we create a new array with new size, then copy the old elements into the new array. Which is computatinally expensive task. In linked lists, we are free to add new elements very directly.

The Memory Mode: Array vs. Linked List

Pointers revisited

Each element in the linked list is denoted by a Node. To connect between nodes, we may use pointers. So, each Node has a pointer pointing to the Next Node. The DNA sequence as a Linked List (LL), can be achieved with the following

struct Node
{
    char data;
    Node* next;
};

The last Node (back)

How to recognize that we are on the latest Node?. In this case, we will make the next pointer equals to nullptr. So we know then we are reached the last element.

For example, if we need to print all elements on a list, we will use this very simple logic:

void printLL( Node* front )
{
    Node *current = front;

    while( current != nullptr )
    {
        std::cout << current->data;
        current = current->next;
    }
}

The LL Structure

We need to make a struct that will define our LL.

Head (front)

If we have a pointer pointing to the first element in our LL, then we have an access to the whole list, because every Node can see the Next Node.

struct CharLinkedList
{
    Node *head;
}

Tail (back)

Tail is a pointer pointing to the last element to the list. So when we add a new element in the list, we are going to use the tail pointer.

So our LL struct is now consisting of:

struct CharLinkedList
{
    Node *head;
    Node *tail;
}

If we need to insert element on the back:

void insertToList( CharLinkedList &list , char newElement )
{
    list.tail->next = new Node{ newElement , nullptr };
    list.tail = list.tail->next;
}

If we only have an access to the head of the LL, or in other words, if we don’t have a tail, and need to insert an element to the back, then we have to start iterating from the front until we reach the last element in the LL.

void insertToList( CharLinkedList &list , char newElement )
{
    Node *current = list.head;
    
    if( current == nullptr )
    {
        current = new Node{ newElement , nullptr };
        list.head = current;
    }
    else
    {
        while( current->next != nullptr )
        {
            current = current->next;
        }
        current->next = new Node{ newElement , nullptr };
    }
}

Queues

Queues are another Abstract Data Type (ADT), that might be implemented using concrete structures like arrays and linked lists. We refer to Queue behaviour by FIFO (first in, first out).

The ADT Queue should satisfy the following requirements (from wikipedia):

• enqueue, which adds an element to the collection end (back), and.
• dequeue, which removes the first element added (front) that was not yet removed.

This makes the queue a First-In-First-Out (FIFO) data structure. In a FIFO data structure, the first element added to the queue will be the first one to be removed. Additionally, a peek operation may give access to the front element without dequeuing it. – Queue (Abstract Data Type)

Home Demo

Open QueueArray and play with the queue to realize its behaviour. This demo shows a Queue implemented with arrays.

More intuition about Queue as ADT

To get more inuition about Queue properties as an ADT:

Biomedical Application: Queues of Biological Signals

Queues as a data structure can be used to represent a time window (interval) of biological signal being displayed on screen.

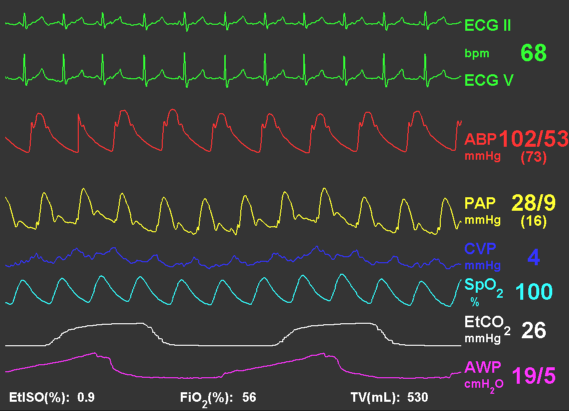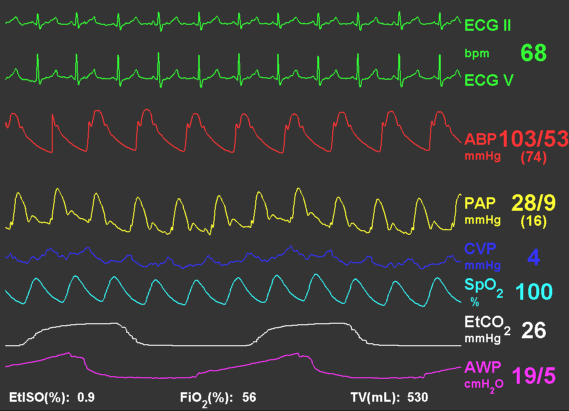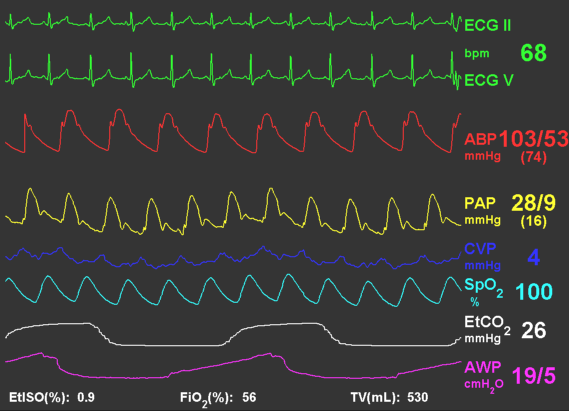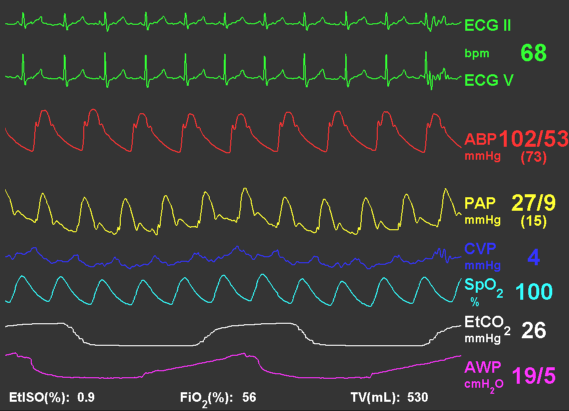
For example, every 10 ms a Queue of ECG signal may enqueue new sample to the back (right to the figure), and dequeue old sample from the front (left to the figure). So, this way you can view an ECG signal of the last 30 seconds. Therefore, we are interested to have a queue with capacity of:

\[\text{Queue (window) size} = \frac{30}{10^{-3}} = 3000 \text{ sample}\]

Implementing Queue using LL

Soon.

Implementing Queue using concrete array

1. The circular buffer

We need to make a buffer (array) with a relatively large capacity for our queue. Let’s make a static array in our box with size 100. Size 100 is the size of the static array, which is the maximum size our Queue can have. Similarly, our Queue is initially empty.

// Let's make a new type for our Queue with a name indicating its properties:
// 1. Our element types are integers.
// 2. The ADT is Queue
// 3. Maximum size is 100
struct DoubleQueue100
{
    double buffer[ 100 ];
    int capacity = 100;
};

Finally, let’s make two variables indicating the front and the back of our Queue

struct DoubleQueue{
    double buffer[ 100 ];
    int capacity = 100;
    int front = -1;
    int back = -1;
};

Making our buffer to act as a circular buffer

We need to make our buffer to be flexible such that we don’t need to shift all elements when we dequeue the front element. Alternatively, we will turn our buffer to a circular buffer using simple logic.

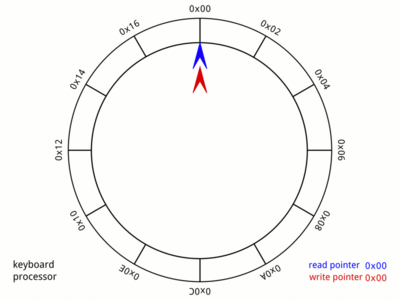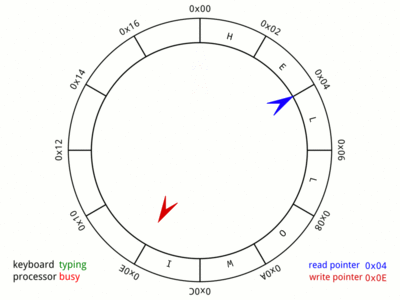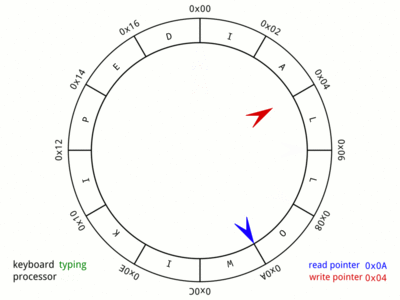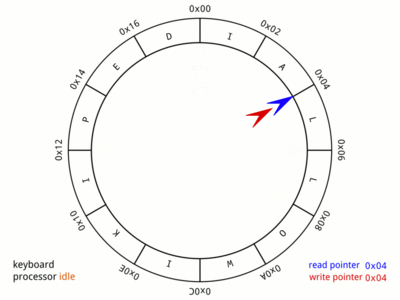
• the blue pointer is the front, where we dequeue elements.
• the red pointer is the back, where we enqueue new elements.