Recursion

\[\begin{eqnarray*} 5! &=& 5 \times 4! \\ 4! &=& 4 \times 3! \\ 3! &=& 3 \times 2! \\ 2! &=& 2 \times 1! \\ 1! &=& 1 \times 0! \\ 0! &=& 1 \end{eqnarray*}\]

Substitute the way back:

\[\begin{eqnarray*} \dot{.\hspace{.095in}.}\hspace{.5in} 1! &=& 1 \times ( 1 ) \\ \dot{.\hspace{.095in}.}\hspace{.5in} 2! &=& 2 \times ( 1 \times 1 ) \\ \dot{.\hspace{.095in}.}\hspace{.5in} 3! &=& 3 \times ( 2 \times 1 \times 1 ) \\ \dot{.\hspace{.095in}.}\hspace{.5in} 4! &=& 4 \times ( 3 \times 2 \times 1 \times 1 ) \\ \dot{.\hspace{.095in}.}\hspace{.5in} 5! &=& 5 \times (4 \times 3 \times 2 \times 1 \times 1 ) \\ &=& 120 \end{eqnarray*}\]

How to make your computer compute any factorial using two lines

#include <iostream>
int factorial( int n )
{
    if( n == 0 )
        return 1;
    else
        return n * factorial( n - 1 );
}

int main()
{
    std::cout << "5!=" << factorial( 5 );
    return 0;
}

factorial(5) 
   factorial(4) 
      factorial(3) 
         factorial(2) 
            factorial(1) 
               return 1 
            return 2*1 = 2 
         return 3*2 = 6 
      return 4*6 = 24 
   return 5*24 = 120

How recursion work in stack memory

Demo: How Recursive Factorial Work in Memory

Recursion is not Function Overloading

The following is not recursion; the function area doesn’t call itself, but it calls another function with the same name, that handles different parameters type/number.

struct Rectangle
{
    double a = 0;
    double b = 0;
};

double area( double a , double b )
{
    return a * b;
}

double area( Rectangle rect )
{
    return area( rect.a , rect.b ); // This is not recursion.
}

However, the following calling area in the next code will results in an infinite loop of recurion, until the stack memory overflows, and finally the program crashes.

struct Rectangle
{
    double a = 0;
    double b = 0;
};

double area( Rectangle rect )
{
    return area( rect ); // This is a recursion. Very pointless and buggy function!
}

Add to your glossary: Stack Memory Overflow

Example: Factorial Function

TODO:Figures

Exercise: Power Function

Implement a function power that uses recursion to compute the power of the input number. After finishing:

  1. initialize a repository on your local machine, git init
  2. add the files to your repository, never add the executable file generated from the compiler, using: git add file1.cpp file2.hpp.
  3. Commit changes: git commit -a -m "add implementation and add files to the repository"
  4. Create remote repository at github, copy the link of your repository from the green button.
  5. link your local repository to the remote repository using: git remote add origin [repo_link].
  6. Push: git push origin master.

Finally, you can send me the link of your repository on github to review!

Very important in Tree Data Structures

Big-Oh Notation

What is an Algorithm

According to Donald Knuth, the word algorithm is derived from the name “al-Khowârizmı̂,” a ninth-century Persian mathematician.

In programming, algorithm is a function with clever logic. However, algorithm is a very general term. The meanArray function you implemented could be called an algorithm to compute the mean of array. Similary, varianceArray, minArray, maxArray, factorial, and power can all be called Algorithms.

We are typically concerned about the function running time when the input size n are relatively large. The measure we are going to study for this semester is called O-notation. O-notation of an algorithm will measure the order of running time growth when the input size n increases.

How to measure an algorithm performance

Measurement should be in terms of the input

For example, applying the function meanArray to compute the mean for array of 10 elements is much faster than computing the mean for array of 10000 elements. So our measurement should respect the input size, or n. Considering n, or the input size, we can measure how the function running time will grow with increase of input size n.

Constant Performance

int sqaure( int x )
{
    int y = x * x; // T1(n) = 1
    return y; // T2(n) = 1
}
\[T(n) = T1 + T2 = 2\] \[O( T(n) ) = O(2) = O(1)\]

When we call this function, we execute two lines, each is a simple experession execution. Time can be measured in terms of $T(n) = 2$. This function will always have a constant behaviour, regardless the input. In big-O notation this function complexity is represented by $O(1)$. We use $O(1)$ to describe the complexity of any function that has a constant execution time.

Other example function with constant complexity

Again, could be done that way:

bool isEmpty( CharacterStackLL &stack )
{
    return stack.front == nullptr; // T(n) = 1
}
\[T(n) = 1\] \[O( T(n) ) = 1\]

This function, isEmpty, has always a constant execution time that doesn’t depend on the stack size n. In other words, its execution time is always constant whether the stack size n=10, n=90, or n=1000.

Synonyms: Performance, Behaviour, Complexity

Linear Performance

Consider the example of printLL that prints all the elements of a LL of size n.

void printLL( Node* front )
{
    Node *current = front; // T1(n) = 1

    while( current != nullptr ) // T2(n) = n * ( T3 + T4 )
    {
        std::cout << current->data; // T3(n) = 1
        current = current->next; // T4(n) = 1
    }
}
\[\begin{eqnarray*} T(n) &=& T1 + T2 \\ &=& 1 + n ( T3 + T4 ) \\ &=& 1 + 2n \end{eqnarray*}\] \[\begin{eqnarray*} O(T(n)) &=& O( 1 + 2n ) \\ &=& O(n) \end{eqnarray*}\]

So this function is asymptotically linear in execution time. We mean by asymptotically linear that we are certain that this function will finally follow a line function for relatively large n.

  • Question: How to approximately estimate the function running time for $n_2=1000000$, i.e linked-list of 1-million element

  • Givens:

    • The function has complexity of $ O(T(n)) = O( 2n + 1 ) = O(n) $.
    • The function executed in 2 melliseconds when $n_1=2000$.
  • Answer:

Because of Linear Performance:

$ \frac{T_{execution}(n_2)}{ T_{execution}(n_1)} \approx \frac{n_2}{n_1}$ ;For relatively large n1, and n2.

\[\begin{eqnarray*} T_{execution}(n_2=1000000) &\approx& \frac{1000000}{2000} T_{execution}(n_1=20) \\ &=& 500 \times 2 = 1 \text{second} \end{eqnarray*}\]
  • Intuition :
\[\begin{eqnarray*} \lim_{\substack{n_1\to\infty\\ n_2\to\infty} } T_{execution}(n_2) &=& \lim_{\substack{n_1\to\infty\\ n_2\to\infty} } \frac{2n_2 + 1}{2n_1 + 1} T_{execution}(n_1) \\ &=& \lim_{\substack{n_1\to\infty\\ n_2\to\infty} } \frac{2n_2}{2n_1} \frac{1 + \frac{1}{2n_2}}{ 1 + \frac{1}{2n_1}} T_{execution}(n_1)\\ &=& \lim_{\substack{n_1\to\infty\\ n_2\to\infty} } \frac{n_2}{n_1} T_{execution}(n_1) \end{eqnarray*}\]

Quadratic Performance

Consider the following naive inefficient function varianceArray

double varianceArray( double *base, int arraySize )
{
    double sum = 0 ; // T1(n) = 1
    for( int i = 0; i < arraySize ; ++i ) // T2(n) = n ( T3 + T4 )
    {
        double diff = meanArray(&base[0],arraySize ) - base[i]; // T3(n) = n
        sum = sum + diff * diff ; // T4(n) = 1
    }
    return sum / arraySize; // T5(n) = 1
}
\[\begin{eqnarray*} T(n) &=& T1 + T2 + T5\\ &=& 1 + n ( T3 + T4 ) + 1\\ &=& 1 + n( n + 1 ) + 1 \\ &=& n^2 + n + 2 \\ O(T(n)) &=& O(n^2 + n + 2) \\ &=& O(n^2) \end{eqnarray*}\]

Further: Orders of Common Function

Orders of common functions

Exercises


// n = input array `basePointer` size
int countCharacter( char *basePointer , int size , char query )
{
    int x = 0; // T1(n) = 1
    for ( int i = 0; i < size; ++i) // T2(n) = n * T3(n)
    {
        if ( query == basePointer[i] ) T3(n) = 1
            ++x;
    }
    return x; //T4(n) = 1
}
// T(n) = T1 + T2 + T4 = 1 + n * T3 + 1 = 2 + n
// O(T(n)) = O(n)

char *analyzeDNA( char *base, int size, int &countA, int &countC, int &countG, int countT)
{
    countA = arrays::countCharacter( &base[0], size, 'A'); // T1(n) = 2 + n => O(n)
    countC = arrays::countCharacter( &base[0], size, 'C'); // T2 = same
    countG = arrays::countCharacter( &base[0], size, 'G'); // T3 = same
    countT = arrays::countCharacter( &base[0], size, 'T'); // T4 = same
    return complementarySequence( &base[0], size); // T5 = 1
}

// T(n) = 4 * (2 + n) + 1 = 9 + 4n
// O(T(n)) = O(n)

Markdown

## How to ask for help like a pro!

1. Write some buggy C++ code.
2. After failed compilation, `git commit -a -m "some bugs to review"`.
3. `git push origin master`.
4. On the last commit, add a comment mentioning me (i.e using `@A-Alaa`).
    * ![rev1](/gallery/review1.png)
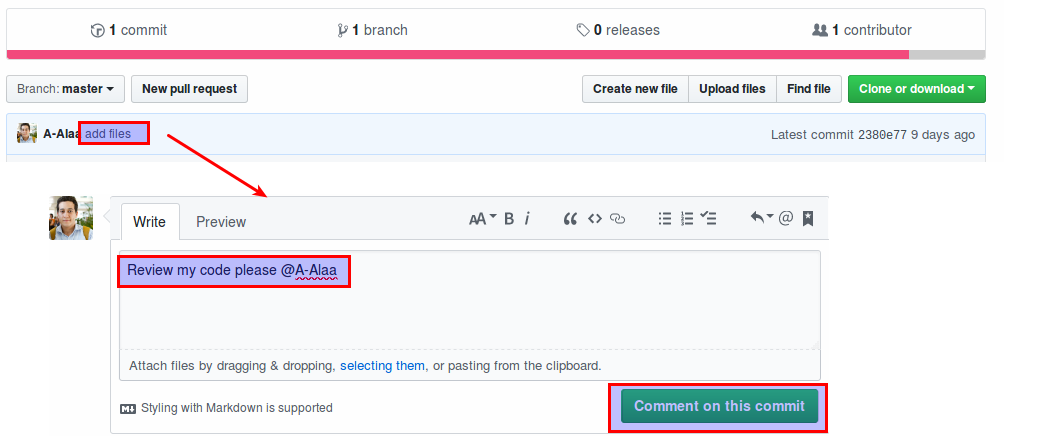
5. Alternatively, after commiting and pushing, ask in O.H about your concerns in the last commit.

## How to bring your TA diabetes

* The easiest way

    1. Write some buggy C++ Code.
        ```c++
        int main()
        {
            int x = y; // who is `y`?!
            return 0 // missing semicolon
        }
        ```
    2. Send the source code file to your TA through e-mail or fb!
* The other way

    1. Write some buggy C++ code.
    2. Compile your source code.
    3. Take screenshot for the compilation error beside your code.
    4. Send through e-mail or fb!

The previous Markdown syntax will generate the following output:

How to ask for help like a pro!

  1. Write some buggy C++ code.
  2. After failed compilation, git commit -a -m "some bugs to review".
  3. git push origin master.
  4. On the last commit, add a comment mentioning me (i.e using @A-Alaa).
    • rev1
  5. Alternatively, after commiting and pushing, ask in O.H about your concerns in the last commit.

How to bring your TA diabetes

  • The easiest way

    1. Write some buggy C++ Code. 
       int main()
 {
     int x = y; // who is `y`?!
     return 0 // missing semicolon
 }
    2. Send the source code file to your TA through e-mail or fb!

  • The other way

    1. Write some buggy C++ code.
    2. Compile your source code.
    3. Take screenshot for the compilation error beside your code.
    4. Send through e-mail or fb!