--- ## Objectives 1. Learn about **heap** structure 1. Implementing **heap** using arrays 1. Implementing **priority queue (ADT)** using **heap** 1. The Shortest Path Problem (TSP) --- ## Heaps * Complete Tree. * Heap Property. #### Glossary * Complete Tree: A balanced tree in which the distance from the root to any leaf is either $log(n)$ or $log(n)-1$. [{source}](https://www.cs.auckland.ac.nz/software/AlgAnim/heaps.html). --- ## Heaps: Cont'd | Conceptual Representation | |---------------------| | 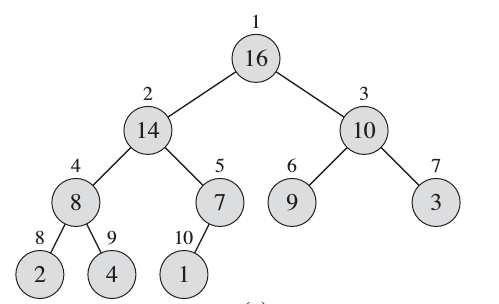 | | 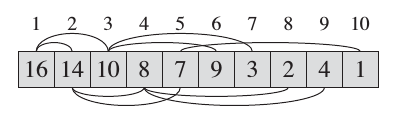 | --- | Heap as array | |---------------| |  | | Creative Commons - [Maxinator](https://commons.wikimedia.org/w/index.php?title=User:Maxiantor&action=edit&redlink=1) | --- ### Operations #### Insert Insertion procedures: -- 1. Insert the new element to the bottom level of the heap. -- 2. Compare the added element with its parent; if they are in the correct order, stop. -- 3. If not, swap the element with its parent and return to the previous step. --- ##### Example: Insert 15 | Layout | |-------| | 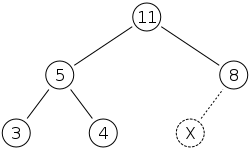 | | Source: [wikipedia](https://en.wikipedia.org/wiki/Binary_heap) | --- ##### Example: Insert - cont'd | Layout | |-------| |  | | Source: [wikipedia](https://en.wikipedia.org/wiki/Binary_heap) | --- ##### Example: Insert - cont'd | Layout | |-------| |  | | Source: [wikipedia](https://en.wikipedia.org/wiki/Binary_heap) | --- #### Extract |Layout | |--------| |  | | Source: [wikipedia](https://en.wikipedia.org/wiki/Binary_heap) | --- #### Extract: cont'd |Layout | |--------| |  | | Source: [wikipedia](https://en.wikipedia.org/wiki/Binary_heap) | --- #### Extract: cont'd |Layout | |--------| |  | | Source: [wikipedia](https://en.wikipedia.org/wiki/Binary_heap) | --- ### Implementation of Min-Heap Using Arrays --- #### Implementation: Buffer  --- ### NOTE We will implement **min-heap**, which has every node's value less then its children. --- #### Implementation: Buffer ```c++ struct Heap { }; ``` --- #### Implementation: Buffer ```c++ struct Heap { std::vector<int> buffer; }; ``` --- #### Implementation: Left Child Index ```c++ int getLeftIdx(int parent) { return ??? } ``` --- #### Implementation: Left Child Index ```c++ int getLeftIdx(int parent) { return parent * 2 + 1; } ``` --- #### Implementation: Right Child Index ```c++ int getRightIdx(int parent) { } ``` --- #### Implementation: Right Child Index ```c++ int getRightIdx(int parent) { return parent * 2 + 2; } ``` --- #### Implementation: Parent Index ```c++ int getParentIdx(int child) { if (child % 2 == 1) { } else { } } ``` --- #### Implementation: Parent Index ```c++ int getParentIdx(int child) { if (child % 2 == 1) { return (child - 1) / 2; } else { } } ``` --- #### Implementation: Parent Index ```c++ int getParentIdx(int child) { if (child % 2 == 1) { return (child - 1) / 2; } else { return (child - 2) / 2; } } ``` --- #### Implementation: Heap size ```c++ int size(Heap &h) { } ``` --- #### Implementation: Heap size ```c++ int size(Heap &h) { return h.buffer.size(); } ``` --- #### Implementation: Insert ```c++ void insert(Heap &h, int data) { h.buffer.push_back(data); } ``` --- #### Implementation: Insert ```c++ void insert(Heap &h, int data) { h.buffer.push_back(data); int childIdx = h.buffer.size() - 1; bubbleUp( h , childIdx ); } ``` --- #### Implementation: Bubble-up / Sift-up / Cascade-up ```c++ void bubbleUp(Heap &h, int child ) { // 1. Do we need parent? // 2. How can we recover heap property. } ``` -- * Guess the steps. --- #### Implementation: Bubble-up / Sift-up / Cascade-up ```c++ void bubbleUp(Heap &h, int child ) { int parent = getParentIdx(child); if( h.buffer[child] < h.buffer[parent]) // Means that heap property is violated { } } ``` -- * The `if` conditions means that Heap property is violated -- * something needs to be done. -- * How to fix? --- #### Implementation: Bubble-up / Sift-up / Cascade-up ```c++ void bubbleUp(Heap &h, int child ) { int parent = getParentIdx(child); if( h.buffer[child] < h.buffer[parent]) { std::swap(h.buffer[child], h.buffer[parent]); // ??? } } ``` -- * Propagate. --- #### Implementation: Bubble-up / Sift-up / Cascade-up ```c++ void bubbleUp(Heap &h, int child ) { int parent = getParentIdx(child); if( h.buffer[child] < h.buffer[parent]) { std::swap(h.buffer[child], h.buffer[parent]); bubbleUp( h , parent ); } } ``` -- * Do we miss anything? --- #### Implementation: Bubble-up / Sift-up / Cascade-up ```c++ void bubbleUp(Heap &h, int child ) { int parent = getParentIdx(child); if( child >= 0 && parent >= 0 && h.buffer[child] < h.buffer[parent]) { std::swap(h.buffer[child], h.buffer[parent]); bubbleUp( h , parent ); } } ``` * Sanity checks. --- #### Implementation: Extract ```c++ int extract(Heap &h) { int child = h.buffer.size() - 1; std::swap(h.buffer[child], h.buffer[0]); int value = h.buffer.back(); h.buffer.pop_back(); bubbleDown( h , 0); return value; } ``` --- #### Implementation: Extract ```c++ int extract(Heap &h) { } ``` --- #### Implementation: Extract ```c++ int extract(Heap &h) { int child = h.buffer.size() - 1; std::swap(h.buffer[child], h.buffer[0]); } ``` --- #### Implementation: Extract ```c++ int extract(Heap &h) { int child = h.buffer.size() - 1; std::swap(h.buffer[child], h.buffer[0]); int value = h.buffer.back(); h.buffer.pop_back(); } ``` --- #### Implementation: Extract ```c++ int extract(Heap &h) { int child = h.buffer.size() - 1; std::swap(h.buffer[child], h.buffer[0]); int value = h.buffer.back(); h.buffer.pop_back(); bubbleDown( h , 0); return value; } ``` --- #### Implementation: Bubble-down / Sift-down / Cascade-down ```c++ void bubbleDown(Heap &h, int parent) { int left = getLeftIdx(parent); int right = getRightIdx(parent); int length = size(h); int minimum = parent; if (left < length && h.buffer[left] < h.buffer[minimum]) minimum = left; if (right < length && h.buffer[right] < h.buffer[minimum]) minimum = right; if (minimum != parent) { std::swap(h.buffer[minimum], h.buffer[parent]); bubbleDown(h, minimum); } else return; } ``` --- ## Clone the source code ```bash git clone git@github.com:sbme-tutorials/sbe201-heap-pq.git ``` --- ## Heapsort | Heapsort | |-----------| | 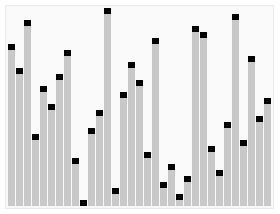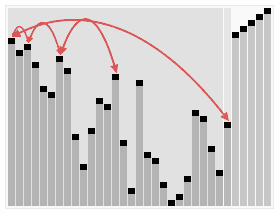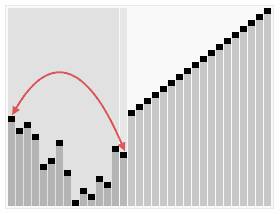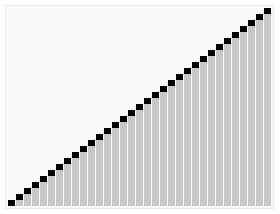 | | Creative Commons - [de:User:RolandH](https://de.wikipedia.org/wiki/User:RolandH) | --- <iframe width="560" height="315" src="https://www.youtube.com/embed/H5kAcmGOn4Q" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen=""></iframe> [{Heaps and Heap Sort}](http://www.zutopedia.com/hs_vs_ms.html) --- ## Reading Homework: Priority Queue (ADT) * What is PQ as an ADT. * How can be implemented using Heap. * Applications. --- ### Reading Homework: Shortest Path Problem * What is shortest path problem. * Dijkstra's algorithm using PQ. * Applications of Dijkstra. --- #### Dijkstra: Exercise 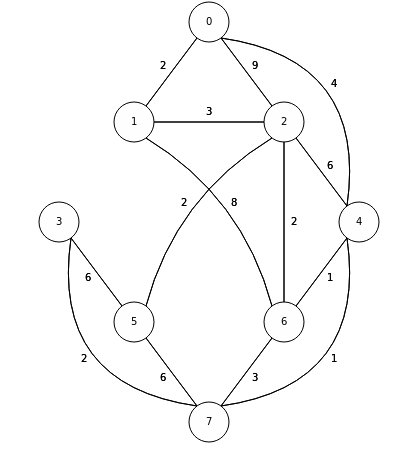 --- #### Dijkstra: Demo <iframe width="560" height="315" src="https://www.youtube.com/embed/U9Raj6rAqqs" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen=""></iframe> --- #### Dijkstra: Application  </textarea> </int>