Week 5: Corner Detection, Laplacian, and Revision Problems

class: top, left
## Corner Detection

By: Asem Alaa

---

class: top, left
## Feature Detection

.center[<img style="width:40%" src="edges-corners.gif">]

---

.center[<img style="width:80%" src="edges-corners2.jpg">]

---

.center[<img style="width:80%" src="edges-corners3.png">]

---
class: top, left

### Challenges

* .red[Patch (image) matching]
--
  * .green[Distinctive features]
--
* .red[Geometric transformations (translation, rotation, scale)]
--
  * .green[Robust and efficient]
--
* .red[Photometric (brightness, exposure)]
--
  * .green[Many preprocessing options can be applied]

---
class: top, left
## Harris operator: corner detector

.center[<img style="width:90%" src="flat-edge-corner.png">]
--

---
## Compute the .red[principal] vectors of variation at location `p`

.center[<img style="width:60%" src="edges_directions.svg">]

---
## Harris operator
### Step 1: image smoothing (optional)

--
$$ L(p,\sigma ) = \[I * G_\sigma \](p) $$

```python
 signal.convolve2d(img, gaussian_kernel(7,1.0) ,'same')
```

.center[<img style="width:50%;" src="image.png">]

---
## Harris operator
### Step 2: compute $I_x$ and $I_y$

Many options to compute the $I_x$ and $I_y$ exist:

1. First order difference.
2. Prewitt kernel
3. Sobel kernel

```python
Ix = signal.convolve2d( img , sobel_h ,'same')
Iy = signal.convolve2d( img , sobel_v ,'same')
```

.center[<img style="width:40%;" src="lx.png"> <img style="width:40%;" src="ly.png">]

---
## Harris operator
### Step3: construct the Hessian (Hesh'n) matrix $M$

We will construct the Hessian matrix so we are able to compute the principal vectors of variation.

--
$$ M(p) = 
\begin{bmatrix}
I_x^2       & I_xI_y \\\
I_xI_y       & I_y^2
\end{bmatrix}
$$

--
```python
Ixx =  np.multiply( Ix, Ix) 
Iyy =  np.multiply( Iy, Iy)
Ixy =  np.multiply( Ix, Iy)
```

---
## Harris operator
### Step3 (Alternative): construct the Hessian (Hesh'n) matrix $M$ .red[over a window]

* If we need more robust detection
--
* Compute $M$ over a window (e.g $3 \times 3$)
--
* Now can detect larger corner that lives inside a window of pixels, instead of a single pixel.

--
$$
\hat{M}(p) = \sum_{i,j}  w(i,j)
\begin{bmatrix}
I_x^2       & I_xI_y \\\
I_xI_y       & I_y^2
\end{bmatrix}
$$

--
$$
\hat{M}(p) =
\begin{bmatrix}
\sum w(i,j) I_x^2(i,j)       & \sum  w(i,j) I_xI_y(i,j) \\\
\sum  w(i,j) I_xI_y(i,j)       & \sum w(i,j) I_y^2(i,j)
\end{bmatrix} 
$$

---
## Harris operator
### Step3 (Alternative): construct the Hessian (Hesh'n) matrix $M$ .red[over a window]

$$
\hat{M}(p) =
\begin{bmatrix}
\hat{I_x^2}       & \hat{I_xI_y} \\\
\hat{I_xI_y}       & \hat{I_y^2}
\end{bmatrix}
$$

--
```python
Ixx =  np.multiply( Ix, Ix) 
Iyy =  np.multiply( Iy, Iy)
Ixy =  np.multiply( Ix, Iy)

Ixx_hat = signal.convolve2d( Ixx , box_filter(3) ,'same') 
Iyy_hat = signal.convolve2d( Iyy , box_filter(3) ,'same') 
Ixy_hat = signal.convolve2d( Ixy , box_filter(3) ,'same') 
```

---
## Harris operator
### Step 4: compute $\lambda_1$ and $\lambda_2$ of $\hat{M}$

* Hessian matrix
<img style="width:50%" src="../../images/Hmat.png">

* Eigen vectors and Eigen values
  * values (amount of variation)
  * vector (variation direction)

.center[<img style="width:50%" src="../../images/eig1.png">]

---

.center[<img style="width:80%" src="screenshot-2.png">]

---
## Harris operator
### Step 4: compute $\lambda_1$ and $\lambda_2$ of $\hat{M}$

--
$$|H - \lambda I | = 0$$

---
## Harris operator
### Interpretation of $\lambda_1$ and $\lambda_2$

.center[<img style="width:70%" src="../../images/eig2.png">]

---
## Harris operator
### Step 5: evaluate corners using $R$ as a measure

--
$$R = (\lambda_1 \times \lambda_2) - k (\lambda_1 + \lambda_2)$$

---
## Harris operator
### Step 4 (Alternative): evaluate $R$ directly without $\lambda_1$ and $\lambda_2$

#### Indirect solution

--
$$det(M) = \lambda_1 \times \lambda_2$$

--
$$trace(M) = \lambda_1 + \lambda_2 $$

--
##### Instead of calculating $\lambda_1, \lambda_2$

--
* $R = det(\hat{M}) - k * trace(\hat{M})$
--
* Trace is sum of diagonal elements

---
## Harris operator
### Step 4 (Alternative): evaluate $R$ directly without $\lambda_1$ and $\lambda_2$

$$
\hat{M}(p) =
\begin{bmatrix}
\hat{I_x^2}       & \hat{I_xI_y} \\\
\hat{I_xI_y}       & \hat{I_y^2}
\end{bmatrix}
$$

$$R = det(\hat{M}) - k * trace(\hat{M})$$

```python
K = 0.05

detM = np.multiply(Ixx_hat,Iyy_hat) - np.multiply(Ixy_hat,Ixy_hat) 
trM = Ixx_hat + Iyy_hat
R = detM - K * trM 
```

---
## Harris operator
### Finally

```python
corners = ???
```

Select large values of $R$, using whatever thresholding heuristic in mind.

#### Thresholding options:
- constant absolute value 
  - (e.g `corners = np.abs(R) > 2.5`)
--
- relative to maximum value 
  - (e.g `corners =  np.abs(R) > 0.2 * np.max(R)`)
--
- relative to quantile value 
  - (e.g `corners =  np.abs(R) > np.quantile(np.abs(R),0.9)`)

```python
corners = np.abs(R) >  np.quantile( np.abs(R),0.999)
```
---
## Harris operator
### Results

--
.center[<img style="width:40%;" src="image.png"> <img style="width:40%;" src="corners.png">]

---

calss: top, left
## FAST Corner Detector
* Features from Accelerated Segment Test (FAST)
* Real-time applications.

<img style="width:100%" src="../../images/fast.png">
---
## FAST Corner Detector
* Basic Algorithm

```python
1. Select Pixel p with intensity $$I_p$$ 
2. Select Threshold t
3. Consider circle with 16 pixels.
4. Calculate absolute difference $$I_p - I_i$$ and i =1 to 16
5. P is a corner if n points have absolute difference > t and n >= 6
6. Suppress weak corners (None-Max suppression)
```

--
* High Speed Test

```python
4. Calculate absolute difference $$I_p - I_i$$ Considering i =1, 9, 5, 13 only.
5. P is a corner if n points have absolute difference > t and n >= 3
6. Suppress weak corners (None-Max suppression)
```
--
* None-Max suppression

```python
For successive corners.
1. For each corner point p
1. Compute score V which is sum of absolute difference between point p and 16 circle points.
2. Suppress if not local maximum. 
```
---
## Otsu Thresholding (segmentation)

.center[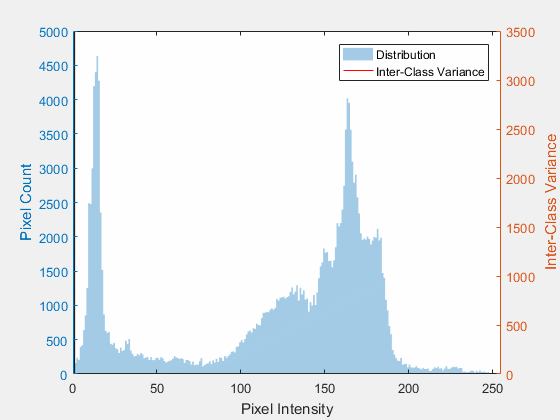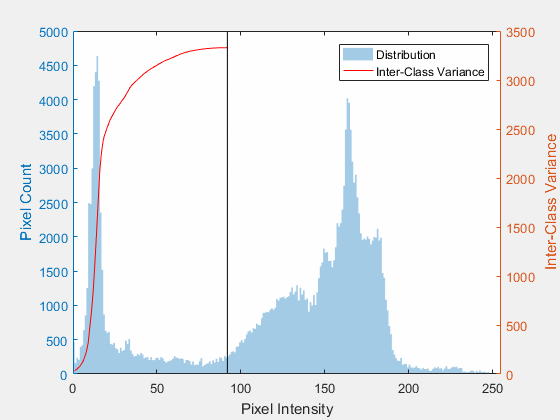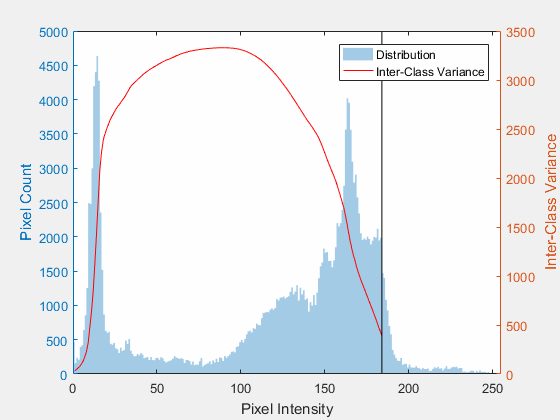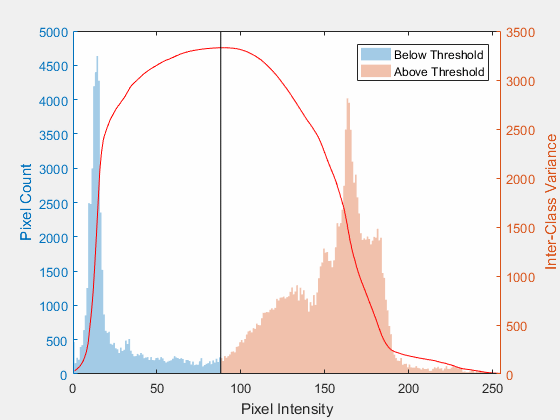![](/2019/cv/images/Otsu's_Method_Visualization.gif)]

---
## Otsu Thresholding (segmentation)
### Minimization of $\sigma_w^2(u)$

$$ \sigma_w^2(u) =  n_1 \sigma_1^2(u)  + n_2 \sigma_2^2(u)  $$

--
* .red[Computation of $\sigma_w^2(u)$ at each $u$ is very costly]
--
* can we do better?

---
## Otsu Thresholding (segmentation)
### Maxmimiztion of $\sigma_b^2(u)$

--
$$ 
\sigma^2 = \sigma_b^2(u) + \sigma_w^2(u) \\\ 
\sigma_w^2(u) = \sigma^2 - \sigma_b^2(u)
$$

--
$\therefore$ minimization of $\sigma_w^2(u)$ = maximization of $\sigma_b^2(u)$

---
## Otsu Thresholding (segmentation)
### Maxmimiztion of $\sigma_b^2(u)$

--
$$ 
\sigma^2 = \sigma_b^2(u) + \sigma_w^2(u) \\\ 
\sigma_w^2(u) = \sigma^2 - \sigma_b^2(u)
$$

--
$\therefore$ minimization of $\sigma_w^2(u)$ = maximization of $\sigma_b^2(u)$

---
## Otsu Thresholding (segmentation)
### Maxmimiztion of $\sigma_b^2(u)$

$$ \sigma_b^2(u) =  n_1 n_2 ( \mu_1(u) - \mu_2(u) )^2  $$

--
.center[![](/2019/cv/images/Otsu's_Method_Visualization.gif)]

---
## Otsu Thresholding (segmentation)
### Python implementation

```python
def otsu_threshold(im):
    # Histogram
    pixel_counts = [np.sum(im == i) for i in range(256)]

s_max = (0,-np.inf)
    
    for threshold in range(256):
        # update
        n1 = sum(pixel_counts[:threshold])
        n2 = sum(pixel_counts[threshold:])

mu_0 = sum([i * pixel_counts[i] for i in range(0,threshold)]) / n1 if n1 > 0 else 0       
        mu_1 = sum([i * pixel_counts[i] for i in range(threshold, 256)]) / n2 if n2 > 0 else 0

# calculate 
        s = n1 * n2 * (mu_0 - mu_1) ** 2

if s > s_max[1]:
            s_max = (threshold, s)
            
    return s_max[0]
```

---
## Otsu Thresholding (segmentation)
### Performance

--
.center[<img style="width:50%;" src="/2019/cv/images/Otsu's_Method_Visualization.gif">]

--
* Maximization of $\sigma_b^2(u)$ is cheaper than minimization of $\sigma_w^2(u)$
--
* But still has quadratic runtime $O(n^2)$
--
* Can we make it linear $O(n)$?!
--
* Submit your answers to `asem.a.abdelaziz@gmail.com`
--
* First two correct answers grants bonus + <img class="emoji" title=":octocat:" alt=":octocat:" src="https://github.githubassets.com/images/icons/emoji/octocat.png" height="20" width="20"> sticker!

---
## Download demos

```
git clone https://github.com/sbme-tutorials/sbe404-harris-otsu-demo.git
```

---
## Midterm Spring 2018 Revision

[{Exam + Model Answers (PDF)}](/2019/cv/presentations/5_week5/SBE404B_Spring2018_MidtermExam_Answer.pdf)

---
## Midterm Spring 2018 Revision

### Q1

<img style="width:60%" src="q1.png">
.smaller[
1. Find the number of gray levels. 
2. Find the image carrier and its cardinality. 
3. What is the number of all possible images that can be defined for this image carrier and numbegray levels?
4. Find the image mean and median. 
5. Find the absolute image histogram.
6. Find the absolute image histogram after the least significant bit is set to 0. In general, what effect would setting to zero the lower-order bit planes have on the histogram of an image?
7. Find the absolute image histogram after the most significant bit is set to 0. In general, what effect would setting to zero the higher-order bit planes have on the histogram of an image?
8. Find and plot the means of the horizontal intensity profiles. 
9. Find the L1 and L2 distances between the first and last vertical intensity profiles. 
]

---
## Midterm Spring 2018 Revision

### Q1

* Find the number of gray levels. 
--
  * .red[8 = $2^3$]
--
* Find the image carrier and its cardinality.
--
  * .red[Image carrier: {$ (x,y) : 1 \leq x \leq 5  \land  1 \leq y \leq 4 $} $\subset Z^2$ ]
  * .red[Cardinality = $5 \times 4 = 20$]
--
* What is the number of all possible images that can be defined for this image carrier and number of gray levels?
--
  * .red[$8^{20}$]
--
* Find the image mean and median.
--
  * .red[mean=3.5, median=3]

---
## Midterm Spring 2018 Revision

### Q1

* .smaller[Find the absolute image histogram.]

--
<img style="width:80%" src="histogram.png">

--
* .smaller[Find the absolute image histogram after the least significant bit is set to 0. In general, what effect would setting to zero the lower-order bit planes have on the histogram of an image?]
--
<img style="width:80%" src="histogram2.png">

--
.red[.smaller[The effect is compressing histogram of the image by clustering each two successive levels to lower one.]]

---
## Midterm Spring 2018 Revision

### Q1

* .smaller[Find the absolute image histogram after the most significant bit is set to 0. In general, what effect would setting to zero the higher-order bit planes have on the histogram of an image?]

--
<img style="width:80%" src="histogram3.png">

--
.red[.smaller[The effect is that the image contrast will decrease and image will be darker.]]

---
## Midterm Spring 2018 Revision

### Q1

* Find and plot the means of the horizontal intensity profiles.

--
.red[| index | horizontal profile mean |
|--|--|
| 1 | 5 |
| 2 | 2.6 |
| 3 | 5.6 |
| 4 | 0.8 |]

---
## Midterm Spring 2018 Revision

### Q1

1. Find the $L_1$ and $L_2$ distances between the first and last vertical intensity profiles. 
  
--
.red[* first column: $a = \[6, 7, 4, 0\]^T $
* last column: $b = \[7, 1, 2, 1 \]^T$]

--
.red[$$L_1 = \frac{1}{4} \sum_0^3 |a_i - b_i| = 2.5 \\\
L_2 = \frac{1}{4} \sqrt{ \sum_0^3 (a_i - b_i)^2 } = 1.5$$]

---
## Midterm Spring 2018 Revision
### Q3

1.  What color would a person see in the first, middle, and last columns of this image? 
2.  What are the cyan (C), magenta (M), and yellow (Y) components of the first, middle, and last columns of this image?
3.  What are the hue (H), saturation (S), and intensity (I) components of the first, middle, and last columns of this image?

---
## Midterm Spring 2018 Revision
### Q3

What color would a person see in the first, middle, and last columns of this image?

1. First: \[.red[1],.green[0],.blue[0]\] (.red[red])
--
2. Middle: \[.red[0.5],.green[1],.blue[0.5]\] (.green[~green])
--
3. Last: \[.red[0],.green[0],.blue[1]\] (.blue[blue])

---
## Midterm Spring 2018 Revision
### Q3

What are the cyan (C), magenta (M), and yellow (Y) components of the first, middle, and last columns of this image?

--
.red[
$$
\begin{bmatrix}
C  \\\
M \\\
Y
\end{bmatrix} = \begin{bmatrix}
1  \\\
1 \\\
1
\end{bmatrix} - 
\begin{bmatrix}
R  \\\
G \\\
B
\end{bmatrix}
$$
]

--
1. First: RGB(1,0,0) => CMY(0,1,1)
--
1. Middle: RGB(0.5,1,0.5) => CMY(0.5,0,0.5)
--
1. Last: RGB(0,0,1) => CMY(1,1,0)

---
## Midterm Spring 2018 Revision
### Q3

What are the hue (H), saturation (S), and intensity (I) components of the first, middle, and last columns of this image?

--
* *See Gonzalez pages 410-411, for conversion formulas*

--
1. First: RGB(1,0,0) => HSI($0,1,\frac{1}{3}$)
--
1. Middle: RGB(0.5,1,0.5) => HSI($\frac{2\pi}{3}, \frac{1}{4}, \frac{2}{3}$)
--
1. Last: RGB(0,0,1) => HSI($\frac{4\pi}{3}, 1, \frac{1}{3} $)

---
## Midterm Spring 2018 Revision
### Q4 - a

The rectangle in the binary image below is of size $4 \times 5$ pixels.

1. What would the magnitude of the gradient of this image look like based on using the approximation
$$ || grad I(x,y) || = |S_x(x,y)| + |S_y(x,y)| $$
Where $S_x$ and $S_y$ are obtained using the Sobel operators. Show all pixel values in the gradient image.

---
## Midterm Spring 2018 Revision
### Q4 - a
#### $S_x$

$$ S_x(x,y) = \[ I *  \begin{bmatrix}
-1 & 0 & 1 \\\
-2 & 0 & 2 \\\
-1 & 0 & 1
\end{bmatrix} \](x,y)$$

--
.center[<img style="width:55%" src="sx.png">]

---
## Midterm Spring 2018 Revision
### Q4 - a
#### $S_y$

$$ S_y(x,y) = \[ I *  \begin{bmatrix}
-1 & -2 & -1 \\\
0 & 0 & 0 \\\
1 & 2 & 1
\end{bmatrix} \](x,y)$$

--
.center[<img style="width:55%" src="sy.png">]

---
## Midterm Spring 2018 Revision
### Q4 - a
#### $|| grad I(x,y) ||$

$$|| grad I(x,y) || = |S_x(x,y)| + |S_y(x,y)|$$

--
.center[<img style="width:55%" src="gradient.png">]

---
## Midterm Spring 2018 Revision
### Q4 - a

Sketch the histogram of the gradient directions $\phi(x, y) = tan^{-1} \frac{S_y (x,y)}{S_x(x,y)}$. Be precise in labeling the height of each component of the histogram.

--
* For each pixel, compute $\phi(x, y)$ that corresponds to a quarter.
--
* histogram: 16 intervals (4 per quarter = 22.5 degree intervals).

---
## Midterm Spring 2018 Revision
### Q4 - a

What would the Laplacian of this image look like based on the following approximation?

* $ \nabla^2 I(x, y ) = I(x + 1, y ) + I(x − 1, y) + I(x, y + 1) + I(x, y − 1) − 4I(x, y)$
--
* **Get the kernel out of it.**
--
* **Convolution**

--
$$L(x,y) =
\[\begin{bmatrix}
0 & 1 & 0 \\\
1 & -4 & 1 \\\
0 & 1 & 0
\end{bmatrix} * I\] (x,y)
$$

---
## Midterm Spring 2018 Revision
### Q4 - a

--
.center[ <img style="width:55%" src="gradient.png"> ]