Week 8 - Part1: Binary Search Trees, Sets (ADT) and Maps (ADT)

## Objectives

1. Learn about **graph** structures in a glimpse
1. Specializing a **graph** into **trees**
1. Specializing **trees** into **binary trees**
1. Specializing **trees** into **binary search trees (BST)**
1. Implementing **set** (ADT) using **BST**

---
## Trees

In previous weeks, we have learned about:

1. Arrays
1. Linked Lists
1. Queues
1. Stacks

* These structures are conceptually linear structures. 
* However, there also exist non-linear (e.g **trees** and **graphs**). 
* **Trees** are special case of **graphs**, where **nodes** and **edges (links)** do not form a cycle.

---
### Tree Glossary

* **Root:** is the top node.
* **Child:** any node that is emerged from an upper node.
* **Parent/Internal Node:** node with at least one child.
* **Siblings:** nodes sharing the same parent.
* **Leaf:** node with no children.
* **Edge:** the link between two nodes.
* **Path:** the sequence of links and nodes to reach from one node to a descedant.
* **Height of node:** the number of links between a node and the furthest leaf.
* **Depth of node:** the number of links between a node and the root.

---
<img src="/gallery/trees/tree.svg" style="width:80%;">

---
### Synonyms

* Node = Vertex = Point
* Edge = Link = Arc

---
### Violating Tree Structure

---
#### The following structures **are not tree**
<img src="/gallery/trees/Directed_graph,_cyclic.svg" style="width:80%;">

---
#### The following structures **are not tree**
<img src="/gallery/trees/Directed_graph_with_branching_SVG.svg" style="height:80%;">

---
#### The following structures **are not tree**
<img src="/gallery/trees/Directed_graph,_disjoint.svg" style="height:80%;">

---
## Binary Search Trees (BST)

* **Binary trees** is a special case of trees where each node can have at most 2 children. 
* Also, these children are named: **left child** or **right child**. 
* A very useful specialization of **binary trees** is **binary search tree (BST)**
* $$ \text{left children} < \text{parent} < \text{right children} $$, 
* and this rule propagates recursively across the tree.

---
<img src="/gallery/trees/Binary_search_tree.svg" style="width:80%;">

---
<img src="/gallery/trees/graphtreevenn.svg" style="width:80%;">

---
### Motivation

Efficient search & insertion/deletion in *logarithmic* time $O(\log(n))$

* Arrays:
  * **(+)** efficient search on sorted arrays $O(\log(n))$,
  * **(-)** ineffiecient insertion/deletion $O(n)$.
* Linked lists:
  * **(-)** inefficient search $O(n)$,
  * **(+)** efficient insertion/deletion $O(1)$.

---
### Intuition

* Tree combines the advantages of arrays and linked lists.
* The nature of **BST** (i.e being ordered) makes it potential for extensive applications.

---
### Design and Implementation: Using Linked Structures

* Recursion: Think of each node in a tree as a separate standalone tree. 
* ADT: Trees can be embedded in arrays or implemented as a linked nodes (i.e using pointers). 
* In this tutorial, we will implement the **BST** using linked nodes. 
* Any node in the tree (including the root) will be represented by the type `BSTNode`

---
#### Node structure

--
```c++
struct BSTNode
{
    int data;
    BSTNode *left;
    BSTNode *right;
};
```

---
### Operations

---
#### Is Empty

--
```c++
bool isEmpty( BSTNode *tree )
{
    return tree == nullptr;
}
```

---
#### Is Leaf

--
```c++
bool isLeaf( BSTNode *tree )
{
    return tree->left == nullptr && tree->right == nullptr;
}
```

---
#### Size

--
```c++
int size( BSTNode *tree )
{
    if ( !isEmpty( tree ) )
        return 1 + size( tree->left ) + size( tree->right );
    else return 0;
}
```

---
#### Insertion

--
<img src="/gallery/trees/binary-search-tree-insertion-animation.gif" style="width:80%;">

---

--
```c++
void insert( BSTNode *&tree, int data )
{
    if ( isEmpty( tree ))
        tree = new BSTNode{ data , nullptr , nullptr };

else
    {
        if ( data < tree->data )
            insert( tree->left, data );

else insert( tree->right, data );
    }
}
```

---
#### Search

---

--
```c++
bool find( BSTNode *tree, int data )
{
    if ( isEmpty( tree ))
        return false;
    else
    {
        if ( data == tree->data )
            return true;

else if ( data < tree->data )
            return find( tree->left , data );

else return find( tree->right , data );
    }
}
```

---
#### BST Traversal

---
#### Traversal: In-order

---

--
```c++
void inorder( BSTNode *tree )
{
    if( tree )
    {
        inorder( tree->left );
        std::cout << "[" << tree->data << "]";
        inorder( tree->right );
    }
}
```

---
#### Traversal: Pre-order

---

--
```c++
void preorder( BSTNode *tree )
{
    if( tree )
    {
        std::cout << "[" << tree->data << "]";
        preorder( tree->left );
        preorder( tree->right );
    }
}
```

---
#### Traversal: Post-order

---

--
```c++
void postorder( BSTNode *tree )
{
    if( tree )
    {
        postorder( tree->left );
        postorder( tree->right );
        std::cout << "[" << tree->data << "]";
    }
}
```

---
#### Traversal: Breadth-first

---
#### Clear the whole tree

--
```c++
void clear( BSTNode *&tree )
{
    if ( !isEmpty( tree ))
    {
        clear( tree->left );
        clear( tree->right );
        delete tree;
        tree = nullptr;
    }
}
```

---
#### Removal of element

---
##### **Case I:** Node to be removed **has no children**

###### Example: `remove( tree , -4 )`

![bst-del1](/gallery/trees/bst-remove-case-1.png)

---
##### **Case II:** Node to be removed **has one child**

###### Example: `remove( tree , 18 )`

---
##### **Case II:** Node to be removed **has one child**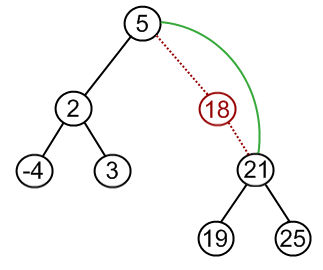
![bst-del2a](/gallery/trees/bst-remove-case-2-1.png)

---
##### **Case II:** Node to be removed **has one child**
![bst-del2b](/gallery/trees/bst-remove-case-2-2.png)

---
##### **Case II:** Node to be removed **has one child**
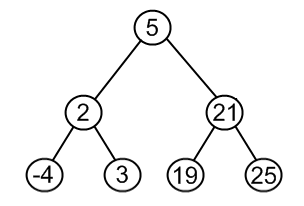![bst-del2c](/gallery/trees/bst-remove-case-2-3.png)

---
##### **Case III:** Node to be removed **has two children**

###### Example: `remove( tree , 18 )`

---
##### **Case II:** Node to be removed **has one child**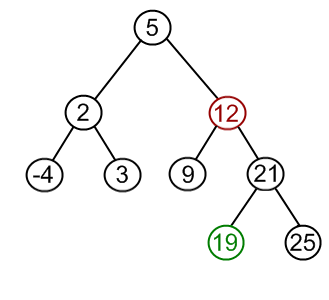
![bst-del3a](/gallery/trees/bst-remove-case-3-3.png)

---
##### **Case II:** Node to be removed **has one child**
![bst-del3b](/gallery/trees/bst-remove-case-3-4.png)

---
##### **Case II:** Node to be removed **has one child**
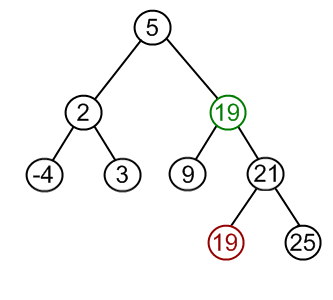![bst-del3c](/gallery/trees/bst-remove-case-3-5.png)

---
##### **Case II:** Node to be removed **has one child**
![bst-del3d](/gallery/trees/bst-remove-case-3-6.png)

---
```c++
void remove( BSTNode *&tree, int data )
{
    if ( isEmpty( tree )) return;
    if ( data == tree->data ) removeNode( tree );
    else if ( data < tree->data ) remove( tree->left, data );
    else remove( tree->right, data );
}
```

---
```c++
void removeNode( BSTNode *&tree )
{
    if ( !isEmpty( tree->left ) && !isEmpty( tree->right ))
    {
        BSTNode *minRight = minNode( tree->right );
        tree->data = minRight->data;
        remove( tree->right, minRight->data );
    } else
    {
        BSTNode *discard = tree;

if ( isLeaf( tree )) tree = nullptr;
        else if ( !isEmpty( tree->left )) tree = tree->left;
        else tree = tree->right;

delete discard;
    }
}
```

---
## Abstract Data Types Built Upon BST

---
### Set

* We can harness the sorted property of **BST** to make efficient insertions and removals. 
* Also, with a slight modification to the `insert` function, we can make this function only insert unique values, 
* hence our new **set (ADT)** will always contain unique values.

---
#### Operations

* `isEmpty`: same as **BST**
* `size`: same as **BST**
* `contains`: same as `find` of **BST**
* `remove`: same as **BST**

---
#### Set: Insert

* Slight modification of `bst::insert`, 
* insertion is done when the element isn't a duplicate of existing element

##### possible implementation:

1. use `contains` to check if element doesn't already exist,
1. then, if the condition holds, use `bst::insert`, otherwise, do nothing.

---
#### Set: Union

* `union`: given two sets $S_1$ and $S_2$ make a new data structure $S_3 = S_1  \cup S_2$

##### possible implementation:

1. make an empty set `S3`,
1. iterate over elements of `S1` inserting each element to `S3`, and similarly for `S2`.

---
#### Set: Intersect

* `intersect`: given two sets $S_1$ and $S_2$ make a new data structure $S_3 = S_1  \cap S_2$

##### possible implementation:
  
1. make an empty set `S3`,
1. iterate over elements of `S1` inserting each element that also exists in `S2` into `S3`.

---
#### Set: Equals

* `equals`: given two sets $S_1$ and $S_2$, check the equality of the two sets,

##### possible implementation:
  
1. first, check that $S_1$ and $S_2$ sizes are equal,
1. then, iterating **in-order** in parallel in both $S_1$ and $S_2$ to validate the equality of traversed elements.

---
### Map

Synonyms: Associative containers, dictionary, symbol table.

A **map** is a collection of searchable key-value pairs, where each key has a value.

---
#### Map: Example 1,

we can have a **map** representing count of words in a page or textbook, so:

1. the **key** here is the *word*, 
1. while the **value** is the count of this word.

---
#### Map: Example 2,

for the function that counts characters in **DNA**:

```c++
int countCharacter( std::string dna, char query )
    {
        int count = 0;
        for ( int i = 0; i < dna.size(); ++i)
        {
            if ( query == dna[i] )
                ++count;
        }
        return count;
}
int main( int argc, char **argv )
{
    if( argc == 2 )
    {
        std::string dna = getDNA( argv[1] );

int countA = countCharacter( dna , 'A');
        int countC = countCharacter( dna , 'C');
        int countG = countCharacter( dna , 'G');
        int countT = countCharacter( dna , 'T');
    }
    return 0;
}
```

---
#### Map: Example 2
##### Elegant solution

* `countCharacter` was called four times (i.e to count **A**, **C**, **G**, and **T**). 
* However, by using **map** data structure we can run this function to count all characters in a single run!

---
```c++
int main( int argc, char **argv )
{
    if( argc == 2 )
    {
        std::string dna = getDNA( argv[1] );

std::map< char, int > dnaCounter;

for( int i = 0 ; i < dna.size() ; ++i )
            dnaCounter[ dna[i] ]++;
    }

return 0;
}
```

---
#### Map: Example3

* Another important usage of **map (ADT)** is to implement a **graph (ADT)** by:

1. representing each node in the graph as a **key**,
1. and the associated **value** to that key is a list of the connected nodes.

---
#### Implementing a Dictionary (i.e Map) Using BST

Map implementation using **BST** would be as easy as implementing a **set** using the concrete routines of **BST**.

1. `create`: returns empty dictionary.
1. `isEmpty`: checks if dictionary is empty.
1. `size`: returns the size of the dictionary.
1. `insert`: inserts new key to the dictionary.
1. `remove`: remove an element by its key.
1. `at`: returns a reference to the value associated with a given dictionary. Crashes if the key is not found.
1. `value`: returns a reference to the value associated with a given key. If key not found, then insert a new key with the given key then returns a reference to the newly created value.
1. `contains`: checks if a key exists in the dictionary.

---
#### Dictionary Node Structure

```c++
struct MapNode
{
    std::string key;
    int value;
    MapNode *left;
    MapNode *right;
};

using WordMap = MapNode *;
```

---
##### Syntactical Sugar

```c++
using WordMap = MapNode *;
```

* make an alias for a pointer type naming it `WordMap`. 
* outside the library, **pay no attention to the implementation details of our map**. 
* We wish not to see any asterisks (pointer) in the main function.
* If we see asterisk in the main function, then we know how this **map** implemented.

---
##### More abstraction

* Since we decided to hide the implementation details in the main function,
* we hope not to initialize an empty **map** using the following syntax:

```c++
int main()
{
    map::WordMap wmap = nullptr; // Correct. But, something vague here!
}
```

* .red[Details are still exposed]
* .red[We know what you did there!]

---
##### More abstraction

**A much better and clean solution**

```c++
WordMap create()
{
    return nullptr;
}
```

```c++
int main()
{
    map::WordMap wmap = map::create(); // Much cleaner!
}
```

---
```c++
bool isEmpty( WordMap wmap )
{

}

bool isLeaf( WordMap wmap )
{

}

int size( WordMap wmap )
{

}

bool find( WordMap wmap, std::string key )
{

}
```

---
```c++
void insert( WordMap &wmap, std::string key )
{

}

void remove( WordMap &wmap, std::string key )
{

}

void clear( WordMap &wmap )
{

}

void printAll( WordMap wmap )
{

}
```

---
#### Map: at & value

```c++
int &at( WordMap wmap, std::string key )
{

}

int &value( WordMap &wmap , std::string key )
{

}
```

---
### Exercise and Assignment: Text Processing

Clone your group lab work and assignment from this [link](https://classroom.github.com/g/JPz8R-yi).

---
Consider the following text for [Carl Sagan](https://en.wikipedia.org/wiki/Carl_Sagan)

> Look again at that dot. That's here. That's home. That's us. On it everyone you love, everyone you know, everyone you ever heard of, every human being who ever was, lived out their lives. The aggregate of our joy and suffering, thousands of confident religions, ideologies, and economic doctrines, every hunter and forager, every hero and coward, every creator and destroyer of civilization, every king and peasant, every young couple in love, every mother and father, hopeful child, inventor and explorer, every teacher of morals, every corrupt politician, every "superstar," every "supreme leader," every saint and sinner in the history of our species lived there on a mote of dust suspended in a sunbeam. The Earth is a very small stage in a vast cosmic arena. Think of the rivers of blood spilled by all those generals and emperors so that, in glory and triumph, they could become the momentary masters of a fraction of a dot. Think of the endless cruelties visited by the inhabitants of one corner of this pixel on the scarcely distinguishable inhabitants of some other corner, how frequent their misunderstandings, how eager they are to kill one another, how fervent their hatreds. Our posturings, our imagined self-importance, the delusion that we have some privileged position in the Universe, are challenged by this point of pale light. Our planet is a lonely speck in the great enveloping cosmic dark. In our obscurity, in all this vastness, there is no hint that help will come from elsewhere to save us from ourselves. The Earth is the only world known so far to harbor life. There is nowhere else, at least in the near future, to which our species could migrate. Visit, yes. Settle, not yet. Like it or not, for the moment the Earth is where we make our stand. It has been said that astronomy is a humbling and character-building experience. There is perhaps no better demonstration of the folly of human conceits than this distant image of our tiny world. To me, it underscores our responsibility to deal more kindly with one another, and to preserve and cherish the pale blue dot, the only home we've ever known.

---
#### Prelimenary Statistics

| Total count of words | count of words after removing duplicates (i.e word set) |
|----------------------|-----------------------|
| 362 | 205 |

---
#### Comparing `std::string`s

```c++
#include <string>
int main()
{
    std::string s1 = "batman";
    std::string s2 = "superman";

int comparison = s1.compare( s2 );
}
```

---
| comparison value | explanation |
|------------------|-------------|
| positive | it means that `s1` comes after `s2` alphabetically, which is not the case |
| negative | it means that `s1` precedes `s2` alphabetically, which is the case |
| 0 | it means that `s1` equals `s2`, which is not the case |

---
#### Lab work: Extract Set of Words in a Text using Set (ADT)

1. Complete the source code in `set.hpp` to produce a **set** of `std::string`s.
1. Complete the source code in `unique_words.cpp` to print the set of words of the given file.

---
#### Group Assignment 1-A: Implement a Dictionary That Maps Characters to Integers

You are required here to develop a dictionary that has `char` as a key and `int` as a value. We will use this dictionary to keep track of each character count.

1. Complete the implementation in `cmap.hpp`, to produce a a dictionary that maps `char` to `int`.
1. Complete the source code in `countDNA.cpp`, to count each base in the given dna file using the developed **dictionary**.

---
#### Group Assignment 2-B: Evaluate the count of each word in a text using Map (ADT)

1. Complete the implementation in the `map.hpp` file to produce a **dictionary** that maps `std::string` to `int`.
1. Complete the source code in `count_words.cpp` to count each word in the given text file.